はじめに
前回までで、太陽と月を考慮した潮汐力の式を求めてみました。
今回はプログラムを書いて、実際の潮位と比較してみます。
実際の値というのは以下の環境庁のサイトのデータになります。
気象庁 | 潮汐・海面水位のデータ 潮位表
気象庁が提供するページです
pythonコードによる実装
pythonコードは以下のようになっています。今回は湘南港の座標を指定し、その地点での潮位を求めてみます。
import math
from dataclasses import dataclass
from datetime import datetime, timedelta, timezone
import pandas as pd
from backports.zoneinfo import ZoneInfo
# ---------------------------
# Constants
# ---------------------------
G = 6.67430e-11 # m^3 kg^-1 s^-2
M_SUN = 1.98847e30 # kg
M_MOON = 7.342e22 # kg
AU = 149597870700.0 # m
R_EARTH = 6371000.0 # m
g0 = 9.80665 # m/s^2
DEG2RAD = math.pi/180.0
# ---------------------------
# Time conversions
# ---------------------------
def to_julian_date(dt: datetime) -> float:
if dt.tzinfo is None:
dt = dt.replace(tzinfo=timezone.utc)
dt = dt.astimezone(timezone.utc)
year = dt.year
month = dt.month
day = dt.day + (dt.hour + (dt.minute + dt.second/60.0)/60.0)/24.0
if month <= 2:
year -= 1
month += 12
A = year // 100
B = 2 - A + (A // 4)
jd = int(365.25*(year + 4716)) + int(30.6001*(month + 1)) + day + B - 1524.5
return jd
def gmst_angle(jd: float) -> float:
T = (jd - 2451545.0)/36525.0
gmst_sec = 67310.54841 + (876600.0*3600 + 8640184.812866)*T + 0.093104*(T**2) - 6.2e-6*(T**3)
gmst_deg = (gmst_sec/240.0) % 360.0
return gmst_deg*DEG2RAD
# ---------------------------
# Sun / Moon positions (low-precision)
# ---------------------------
def sun_eci(jd: float):
T = (jd - 2451545.0)/36525.0
M = (357.52911 + 35999.05029*T - 0.0001537*T*T) % 360.0
L0 = (280.46646 + 36000.76983*T + 0.0003032*T*T) % 360.0
C = (1.914602 - 0.004817*T - 0.000014*T*T)*math.sin(DEG2RAD*M) \
+ (0.019993 - 0.000101*T)*math.sin(DEG2RAD*2*M) \
+ 0.000289*math.sin(DEG2RAD*3*M)
true_long = (L0 + C) % 360.0
R_au = 1.000001018*(1 - 0.01670862*math.cos(DEG2RAD*M) - 0.00004204*math.cos(DEG2RAD*2*M))
R = R_au*AU
eps = 23.439291 - 0.0130042*T
lam = DEG2RAD*true_long
epsr = DEG2RAD*eps
x_ecl = math.cos(lam)
y_ecl = math.sin(lam)
z_ecl = 0.0
x = R * x_ecl
y = R * (y_ecl*math.cos(epsr))
z = R * (y_ecl*math.sin(epsr))
return x,y,z,R
def moon_eci(jd: float):
T = (jd - 2451545.0)/36525.0
Lp = (218.3164477 + 481267.88123421*T - 0.0015786*T*T + T**3/538841.0 - T**4/65194000.0) % 360.0
D = (297.8501921 + 445267.1114034*T - 0.0018819*T*T + T**3/545868.0 - T**4/113065000.0) % 360.0
Mp = (134.9633964 + 477198.8675055*T + 0.0087414*T*T + T**3/69699.0 - T**4/14712000.0) % 360.0
F = (93.2720950 + 483202.0175233*T - 0.0036539*T*T - T**3/3526000.0 + T**4/863310000.0) % 360.0
lon = Lp + 6.289*math.sin(DEG2RAD*Mp) + 1.274*math.sin(DEG2RAD*(2*D - Mp)) \
+ 0.658*math.sin(DEG2RAD*(2*D)) + 0.214*math.sin(DEG2RAD*(2*Mp)) + 0.110*math.sin(DEG2RAD*D)
lat = 5.128*math.sin(DEG2RAD*F) + 0.280*math.sin(DEG2RAD*(Mp+F)) + 0.277*math.sin(DEG2RAD*(Mp-F)) \
+ 0.173*math.sin(DEG2RAD*(2*D - F))
dist_km = 385001.0 - 20905.0*math.cos(DEG2RAD*Mp) - 3699.0*math.cos(DEG2RAD*(2*D - Mp)) \
- 2956.0*math.cos(DEG2RAD*(2*D)) - 570.0*math.cos(DEG2RAD*(2*Mp))
A = dist_km * 1000.0
eps = (23.439291 - 0.0130042*T)*DEG2RAD
lam = lon*DEG2RAD
beta = lat*DEG2RAD
x_ecl = math.cos(beta)*math.cos(lam)
y_ecl = math.cos(beta)*math.sin(lam)
z_ecl = math.sin(beta)
x = A*x_ecl
y = A*(y_ecl*math.cos(eps) - z_ecl*math.sin(eps))
z = A*(y_ecl*math.sin(eps) + z_ecl*math.cos(eps))
return x,y,z,A
def eci_to_ecef(vec, jd):
theta = gmst_angle(jd)
c, s = math.cos(theta), math.sin(theta)
x,y,z = vec
xe = c*x + s*y
ye = -s*x + c*y
ze = z
return xe, ye, ze
def surface_unit_ecef(lat_deg, lon_deg):
lat = lat_deg*DEG2RAD
lon = lon_deg*DEG2RAD
cl, sl = math.cos(lat), math.sin(lat)
cln, sln = math.cos(lon), math.sin(lon)
x = cl*cln
y = cl*sln
z = sl
return x, y, z
def P2(mu):
return 0.5*(3*mu*mu - 1.0)
@dataclass
class TideParams:
h2: float = 1
g: float = g0
R: float = R_EARTH
def vertical_tide_displacement(lat_deg, lon_deg, dt, params: TideParams = TideParams()):
jd = to_julian_date(dt)
sx, sy, sz, As = sun_eci(jd)
mx, my, mz, Am = moon_eci(jd)
sxe, sye, sze = eci_to_ecef((sx,sy,sz), jd)
mxe, mye, mze = eci_to_ecef((mx,my,mz), jd)
s_norm = math.sqrt(sxe*sxe + sye*sye + sze*sze)
m_norm = math.sqrt(mxe*mxe + mye*mye + mze*mze)
shat = (sxe/s_norm, sye/s_norm, sze/s_norm)
mhat = (mxe/m_norm, mye/m_norm, mze/m_norm)
rx, ry, rz = surface_unit_ecef(lat_deg, lon_deg)
mu_s = rx*shat[0] + ry*shat[1] + rz*shat[2]
mu_m = rx*mhat[0] + ry*mhat[1] + rz*mhat[2]
R = params.R
g = params.g
h2 = params.h2
sun_fac = G*M_SUN / (s_norm**3)
moon_fac = G*M_MOON / (m_norm**3)
zeta = (h2/g * ( (sun_fac)*(R*R)*P2(mu_s) + (moon_fac)*(R*R)*P2(mu_m) ))* 100
return {"datetime_jp": dt.astimezone(ZoneInfo("Asia/Tokyo")).isoformat(),
"lat_deg": lat_deg, "lon_deg": lon_deg,
"zeta_cm": zeta,
"mu_sun": mu_s, "mu_moon": mu_m,
"sun_distance_m": s_norm, "moon_distance_m": m_norm}
# ---------------------------
# Main: simulate
# ---------------------------
if __name__ == "__main__":
lat_demo = 35.68
lon_demo = 139.76
# 湘南港
# 35.300460959728326, 139.48380592606864
lat_demo = 35.300460959728326
lon_demo = 139.48380592606864
start = datetime(2025, 1, 1, 0, 0, 0, tzinfo=timezone.utc)
rows = []
for h in range(744):
dt = start + timedelta(hours=h)
rows.append(vertical_tide_displacement(lat_demo, lon_demo, dt))
df_zeta = pd.DataFrame(rows)
df_zeta["datetime_jp"] = pd.to_datetime(df_zeta["datetime_jp"])実際の値との比較
実際の値と比較すると以下のようになりました。
まずは環境庁から持ってきたデータ。
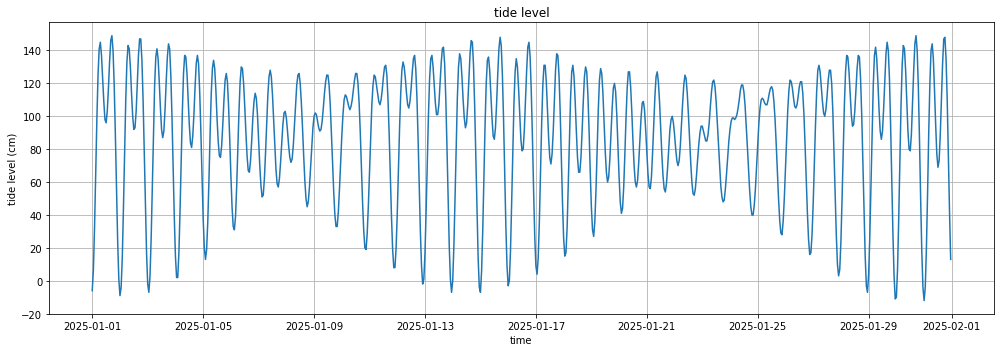
次に今回プログラムで求めた値のグラフです。
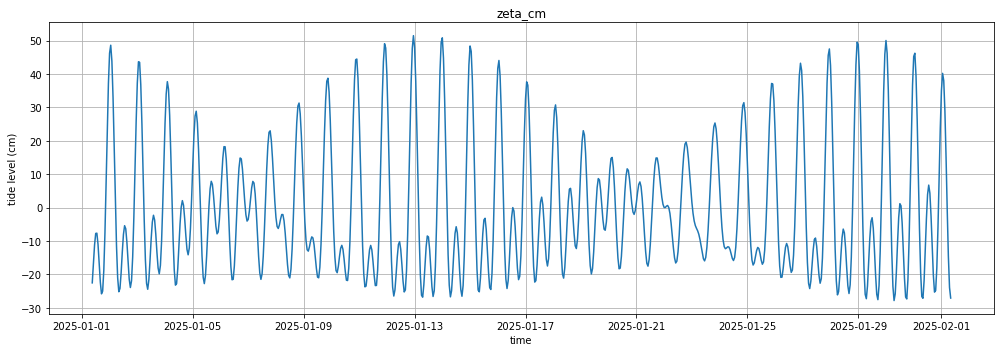
ちょっとわかりにくいので、比べてみます。
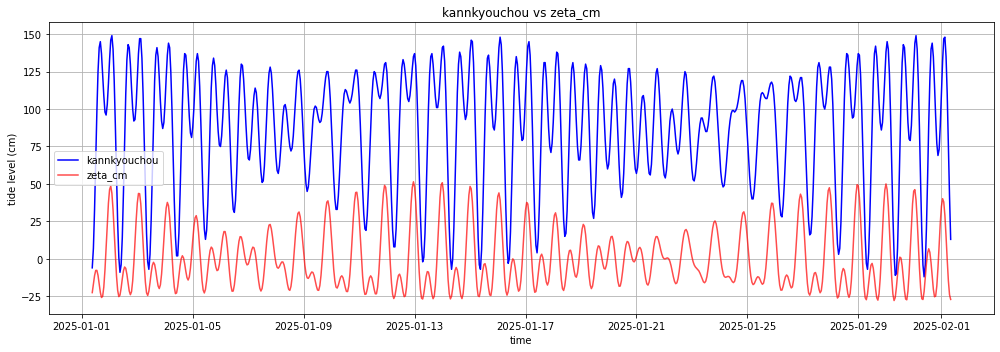
周期としては同じくらいですが、潮位が100cmぐらいずれています。。。
青が環境庁のデータで、赤が今回計算して求めた値のグラフです。
見直しが必要ですね。。。
考察
ChatGPTに聞きつつ、今回の100cmの差異に関して考察をまとめました。
ChatGPT曰くですが、「平衡潮モデル=天体ポテンシャルから理想的に計算した値と実際の潮位=海洋の動力学+地形+共振+気象などの複雑な効果は別物なので、100cm 程度の差が出るのは普通」とのことでした。
このため、計算は正しいはずです。
今回の100cmの差が出る理由としては以下が挙げられるとのことです。
- 平衡潮モデルが前提になっているため
- 海は「均一で大きな浅い水槽」としており、局所の増幅や遅れを無視しているため、位相はおおむね合うことが多いが、振幅は小さく出ることが多い
- 実際は海底地形・湾の共振(地形増幅)があるため
- 狭い入江や湾は共振して潮汐振幅が大きくなる(例:英仏海峡、東京湾の一部など)
- 今回は海洋動力学(流れ・遅れ位相)が考慮されていないため
- 慣性力・コリオリ力・境界層摩擦などで潮汐波が変形・増幅する
- また潮汐成分ごとに伝播・減衰が違う
- 自己引力を考慮していない
- 潮汐は「外力に対する応答」だが、応答した水自身が 新たな重力源 になるので、それが考慮できていない
- Love数の不適合
- Love数とは「地球がどれくらい変形し、重力場がどれくらい変わるか」を表す無次元定数
- 気象(気圧・風)などの非天文要因
- 低気圧、長周期の潮汐津波などで一時的に数十〜数百 cm 変わることもある
最後に
天体にしか着目せずに計算して出した値だから1mほどの誤差が生まれたと結論付けられそうです。
気象庁のサイトではある特定の港でしか見ていないので、座標指定して潮位の推移を見れるようにできたらいいなと思っていたのですが、難しかったです。