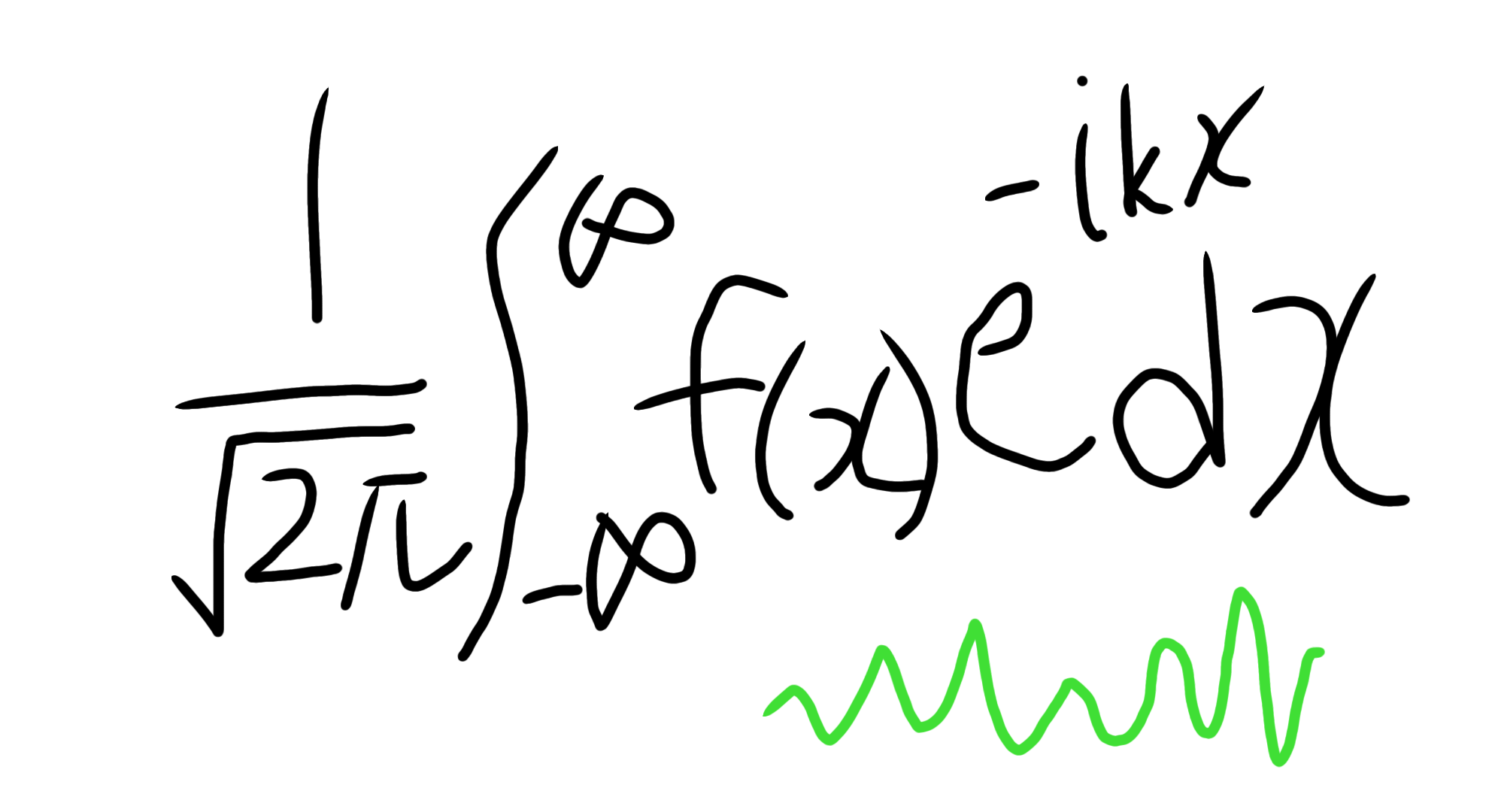はじめに
前回はフーリエ級数展開の式を求めました。
さて、前回までのフーリエ級数で展開できるのは以下のような周期的な関数のみです。
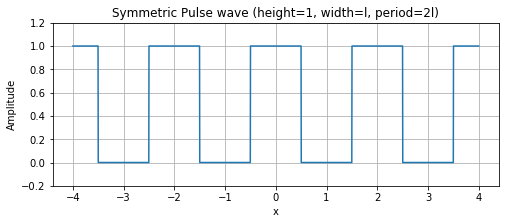
以下のような単一のパルスのような関数にも使える方法がフーリエ変換です。
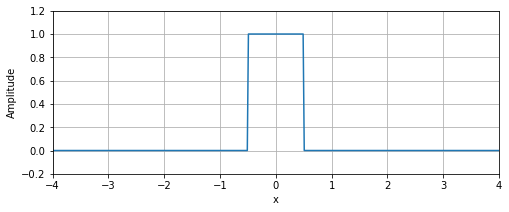
今回はこの単一パルスのような関数にも使えるフーリエ変換を導くところまでやってみます。
周期の拡張
前回までのフーリエ級数展開の式を以下に示します。
$$ f(\theta) = \sum_{n=\infty}^{\infty} c_ne^{in\theta} $$
$$ c_{n}= \frac{1}{2\pi}\int_{-\pi}^{\pi} f(\theta)e^{-in\theta}\, d\theta $$
この式の周期を$2\pi$から$2L$へ拡張します。
$-\pi\le\theta\le\pi$⇒$-L\le x\le L$に変換するとき、$x\equiv\frac{L\theta}{\pi}$となります。
これを$x$を$\theta$で微分してみると$\frac{dx}{d\theta}= \frac{L}{\pi}$⇔$d\theta= \frac{\pi}{L}dx$になります。
これで、以下の3つの式が求まります。
①$$ a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{n\theta}\, d\theta = \frac{1}{\pi}\int_{-L}^{L} f(\frac{\pi x}{L})\cos{(\frac{n\pi x}{L})}\, dx = \frac{1}{L}\int_{-L}^{L} \tilde{f}(x)\cos{(\frac{n\pi x}{L})}\, dx $$
②$$ b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\sin{n\theta}\, d\theta = \frac{1}{\pi}\int_{-L}^{L} f(\frac{\pi x}{L})\sin{(\frac{n\pi x}{L})}\, dx= \frac{1}{L}\int_{-L}^{L} \tilde{f}(x)\sin{(\frac{n\pi x}{L})}\, dx $$
③$$c_n = \frac{1}{2\pi}\int_{-L}^{L} f(\frac{\pi x}{L})e^{-\frac{in\pi x}{L}}\, dx=\frac{1}{2L}\int_{-L}^{L} \tilde{f}(x)e^{-\frac{in\pi x}{L}}\, dx$$
フーリエ級数にパルス波の値を入れる
高さ1、幅$l$、周期$2l$のこの記事の冒頭でも示した以下のようなパルス波を考えてみます。

このパルス波はフーリエ級数は③をつかって
$$c_n = \frac{1}{2l}\int_{-l}^{l} \tilde{f}(x)e^{-\frac{in\pi x}{l}}\, dx = \frac{1}{2l}\int_{-l}^{l} \tilde{f}(x)(cos\frac{n\pi x}{l}-isin\frac{n\pi x}{l})\, dx $$
となります。
このグラフ$\tilde{f}(x)$は原点0で左右対象の線対称となってます。
つまり偶関数です。
また、cosは偶関数、sinは奇関数です。
偶関数×機関数は0なので$c_n$は
$$c_n = \frac{1}{2l}\int_{-l}^{l} \tilde{f}(x)cos\frac{n\pi x}{l}\, dx $$
となります。
また、上記パルス波は$ -\frac{l}{2} \leq x \leq \frac{l}{2} $の範囲で1になっていて、それ以外の範囲で0になっています。
よって、それ以外の0の部分を無視できるので、
$$c_n = \frac{1}{2l}\int_{-\frac{l}{2}}^{\frac{l}{2}} \tilde{f}(x)cos\frac{n\pi x}{l}\, dx $$
この積分を実際に解くと、
$$c_n = \frac{1}{n\pi}\sin\frac{n\pi}{2}\, dx $$
これは$n$が分母にあり、$n=0$の時も考えることが必要で、$n=0$の時は、
$$c_n = \frac{1}{2l}\int_{-\frac{l}{2}}^{\frac{l}{2}} \tilde{f}(x)cos0\, dx $$
なので、これを計算すると、$\frac{1}{2}$になります。
点としてプロットすると、$c_n$の値は
$$
\begin{aligned}
c_{-3} &= \frac{1}{3\pi}, \\\\
c_{-2} &= 0, \\\\
c_{-1} &= \frac{1}{\pi}, \\\\
c_0 &= \frac{1}{2}, \\\\
c_1 &= \frac{1}{\pi}, \\\\
c_2 &= 0, \\\\
c_3 &= -\frac{1}{3\pi}. \\\\
\end{aligned}
$$
のようになり、グラフは以下のようになります。
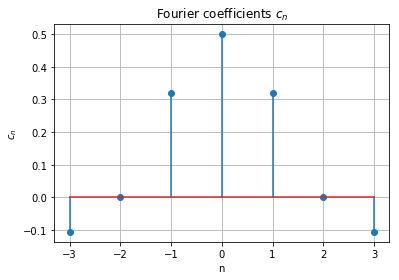
周期の広げる
ここまでは、周期$2l$を考えましたが、次は周期を広げて$4l$を考えてみます。
つまり以下のようなパルス波です。
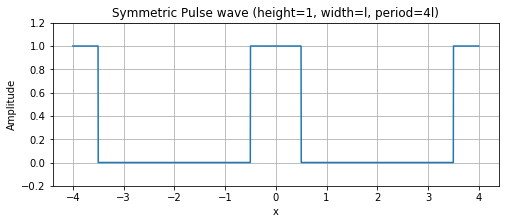
この時、フーリエ級数の式は以下のようになります。
$$c_n = \frac{1}{4l}\int_{-2l}^{2l} \tilde{f}(x)cos\frac{n\pi x}{2l}\, dx $$
ここでも、パルス波は$ -\frac{l}{2} \leq x \leq \frac{l}{2} $の範囲で1になっていて、それ以外の範囲で0になっていることが分かります。
よって、それ以外の0の部分を無視できるので、
$$c_n = \frac{1}{4l}\int_{-\frac{l}{2}}^{\frac{l}{2}} \tilde{f}(x)cos\frac{n\pi x}{2l}\, dx = \frac{1}{n\pi}\sin\frac{n\pi}{4} $$
となります。また$n=0$の時は$\frac{1}{4}$になります。
これを$c_n$を点としてプロットすると、以下のようになります。
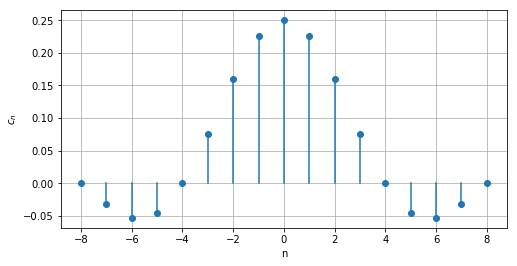
何か、うっすらとグラフが見えてきましたね。
さらに周期を広げる
さらに周期を広げると、以下のような単一パルスのようなパルスになりますね。

ここでは一旦、周期が$2ml$の場合を考えます。
この時$c_n$は
$$c_n = \frac{1}{n\pi}\sin\frac{n\pi}{2m} $$
で$c_0=\frac{1}{2m}$になります。
m=10の時は以下のようなグラフになります。
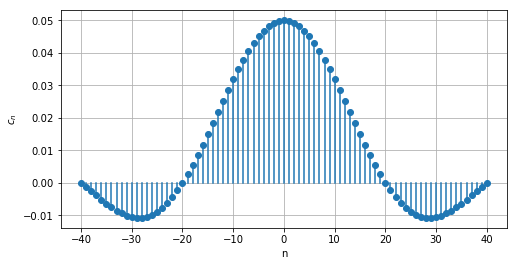
連続のグラフに近づいていることがわかります。
mを無限に飛ばすことで、$\Sigma$を積分として表せます。
つまり、周期$2ml$の場合のフーリエ級数は
$$ f(x) = \sum_{n=-\infty}^{\infty} c_ne^{\frac{in\pi x}{ml}} $$
とした時、積分にして以下のようになります。
④$$ f(x) = \sum_{n=-\infty}^{\infty} c_ne^{\frac{in\pi x}{ml}} = \int_{-\infty}^{\infty} c_n e^{\frac{in\pi x}{ml}}\, dn$$
ここまでが$\Sigma$から積分に変わる話です。
📜📜📜
さて、ここで、③の式より、$L=ml$の場合を考えると、$c_n$は
⑤$$ c_n = \frac{1}{2ml}\int_{-ml}^{ml} {f}(x)e^{-\frac{in\pi x}{ml}}\, dx $$
で、$k=\frac{n\pi}{ml}$とすると、$\frac{dk}{dn}=\frac{\pi}{ml}$となり、これを使うと④と⑤はそれぞれ以下にのようになります。
⑥$$ f(x) = \sum_{n=-\infty}^{\infty} c_ne^{\frac{in\pi x}{ml}} = \int_{-\infty}^{\infty} c_n e^{\frac{in\pi x}{ml}}\, dn =\int_{-\infty}^{\infty} c_n e^{ikx}\frac{ml}{\pi}\, dk $$
⑦$$ c_n = \frac{1}{2ml}\int_{-ml}^{ml} {f}(x)e^{-\frac{in\pi x}{ml}}\, dx = \frac{1}{2ml}\int_{-ml}^{ml} {f}(x)e^{-ikx}\, dx $$
⑥の式に⑦の式を代入して整理すると、
$$ f(x) = \int_{-\infty}^{\infty} (\frac{1}{2ml}\int_{-ml}^{ml} {f}(x)e^{-ikx}\, dx) e^{\frac{ikx}{ml}}\frac{ml}{\pi}\, dk = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} (\frac{1}{\sqrt{2\pi}}\int_{-ml}^{ml} {f}(x)e^{-ikx}\, dx) e^{ikx}\, dk $$
📜📜📜
ここで上記の単一パルスを考える場合は$m$を無限にとばので、
$$ f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} (\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} {f}(x)e^{-ikx}\, dx) e^{ikx}\, dk $$
となります。
これが、単一パルスにも対応できるようにしたフーリエ変換です。
この式を以下のように分解してそれぞれフーリエ変換と逆フーリエ変換の式の出来上がりです。
■フーリエ変換
$$ F(k) \equiv \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} {f}(x)e^{-ikx}\, dx $$
■フーリエ逆変換
$$ f(x) \equiv \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} F(k)e^{ikx}\, dk $$
最後に
フーリエ変換まで求められました!やったー!