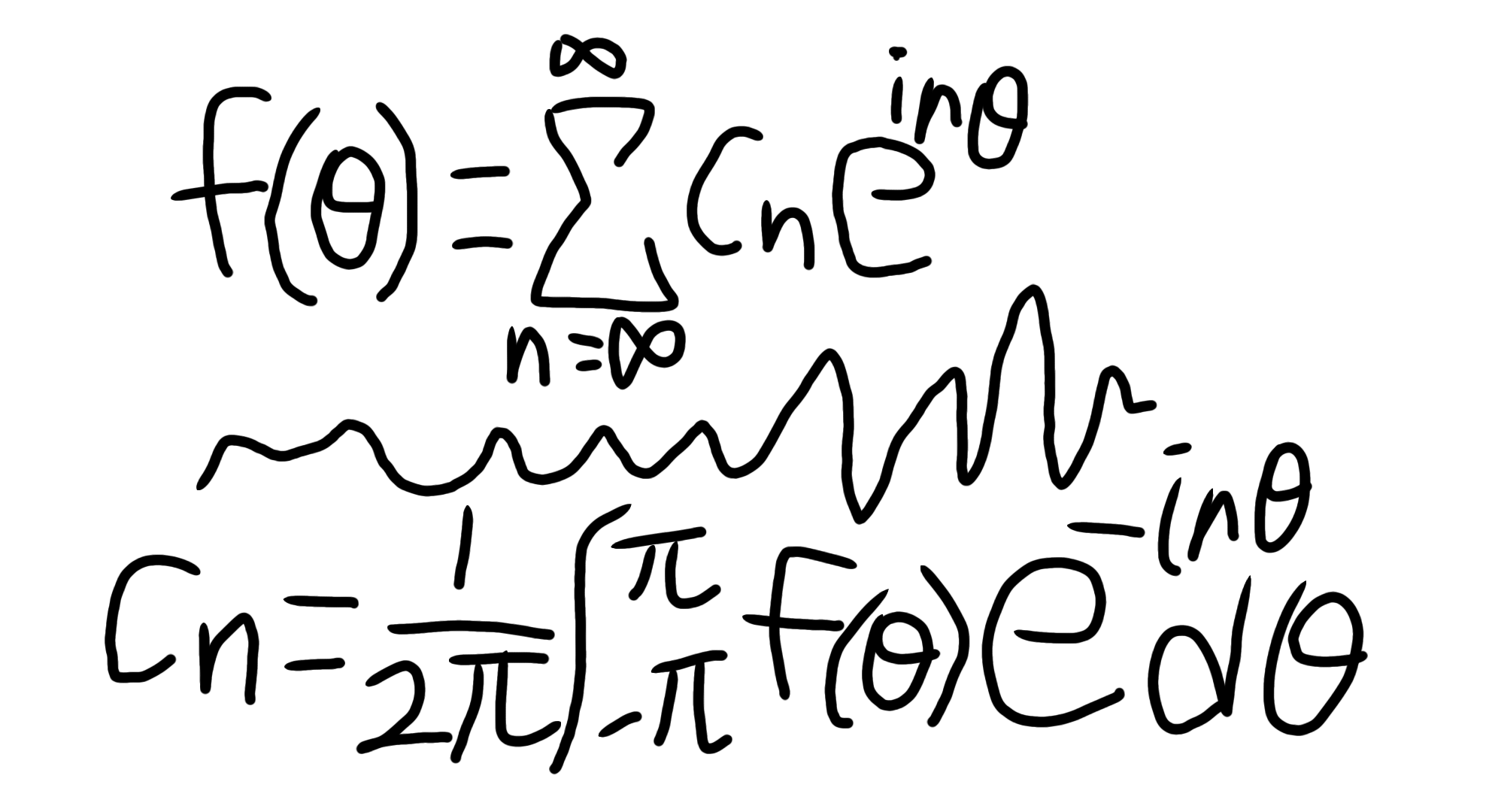はじめに
日常では答えのない問題が多くあり、疲れた僕は数学を勉強することに楽しさすらも覚えていました。
数学を解きたくなるときは、答えの出ない議論が頭の中を反芻する時であり、そんな時に自分の手でノートに数式を書きながら一つの答えにたどり着いたときは心地よい感覚を覚えます。
また、達成感も味わえます。
この達成感の積み重ねが自信になったりするんじゃないか?って思ったりします。
数学は無料でできるパズルです。ジグソーパズルを購入しなくても、プラモデルを購入しなくてもできるパズルです。
しかも場所を取らない。
なんてコスパの良いパズルなのでしょうか。
ある日出会った、数学検定1級のページにあったこの問題。
次の値を求めなさい。ただし、$\sin{z}$、$\cos{z}$はそれぞれ複素数$z$に関する正弦関数、余弦関数で、$i$は虚数単位を表します。
$$ \cos{6i}-i\sin{6i} $$
元のファイルは以下です。
解答は以下のようになります。
解答
まず、
① $\cos{\theta}=\frac{e^{i\theta}+e^{-i\theta}}{2} $
②$\sin{\theta}=\frac{e^{i\theta}-e^{-i\theta}}{2 i} $
という事が成り立つことを知っている必要があります。
これは何故かと言うと、オイラーの公式③$e^{i\theta}=\cos{\theta}+i\sin{\theta}$から
④ $ e^{-i\theta}=\cos{\theta}-i\sin{\theta} $
も求まり、③と④の式を足し算して変形すると①の式が、③と④の式を引き算して変形すると②の式が求まるからです。
オイラーの公式の導出
このオイラーの公式は暗記していないといけないかと言われると一応導出はできます。
$e^{i x}$をテイラー展開すると、
$$ e^{i x}=\sum_{n=0}^{\infty} \frac{(i x)^n}{n!} = 1 + ix – \frac{x^2}{2!} – i\frac{x^3}{3!} + \frac{x^4}{4!} + i\frac{x^5}{5!} – \cdots $$
になります。
この実数部分と虚数部分に分けた時、
$e^{ix}= \left(\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k}}{(2k)!}\right)
+ i\left(\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k+1}}{(2k+1)!}\right)$
この実数部分は$\cos{x}$のテイラー展開をした式で、虚数部分は$\sin{x}$をテイラー展開した式になります。
(ここではテイラー展開の説明は割愛します。)
このため、$e^{ix}=\cos{x} + i\sin{x}$が求まります。
$ \cos{6i} = \frac{e^{i(6i)}+e^{-i(6i)}}{2} $、$ \sin{6i} = \frac{e^{i(6i)}-e^{-i(6i)}}{2i} $
となり、
$ \cos{6i}-i\sin{6i}= \frac{e^{i(6i)}+e^{-i(6i)}}{2} – \frac{i(e^{i(6i)}-e^{-i(6i)})}{2i} = e^{6}$
が答えとなります。
この複雑な式を介して一つのシンプルな答えにたどり着く過程は結構美しく感じます。
複素関数の美しさに触れる
上記でも記載の通り、オイラーの公式は世界一美しい式と言われています。
そもそも指数関数と三角関数が複素数$i$によって繋がるところも感動的なのですが、
$ \theta = \pi$のとき$e^{i\pi}=1$が成り立ち、これは世界で最も美しい等式として知られています。
その理由は、解析の定数$e$と幾何の定数$\pi$と代数学で「完全性」を保証するために必要な$i$が一つのシンプルな式に収まっているからです。
オイラーの公式は複素数の方程式ですが、複素数もその美しさを秘めています。
以下は複素数の美しさに触れられる動画です。
複素数を色々な方法で可視化 | 鑑賞して楽しむ虚数の幻想世界 | VISUALIUM
いつか、僕も複素数のシミュレーションはやってみたいです。
フーリエ変換(序):フーリエ級数
かなり前置きが長くなってしまいましたが、複素関数を扱う方程式で、フーリエ変換というものがあります。
ちらっと見ると以下のような式です。
⑥ $ F(k) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(x)\, e^{-i x k} \, dx $
フーリエ変換とはざっくり言うと、どんな複雑な波形でもsin関数とcos関数で表せるものです。
フーリエ変換の式(⑥)を見るとsin関数とcos関数で表されてはいませんね。
これは上記でも記載の通り、複素数を使用していることで、sin関数とcos関数の複雑な式を簡略化できているわけです。
ちなみに3Blue1Brownの日本版のチャネルでもこのフーリエ変換の内容が視覚的に分かりやすく説明されています。
この複雑なsin関数とcos関数が複素数によって綺麗に整う感覚を味わいたいがためにフーリエ変換まで求めようと思います。
といっても、長くなるので、今回はフーリエ級数展開で複素数を使用するところまでです。
フーリエ級数の始まり
まず、フーリエ級数の最初のアイディアはベルヌーイが弦の振動がsinとcosの足し合わせで表せるのではないかという着想からスタートします。
つまり以下の式である関数$f(\theta)$が表せるのではないかと言う事です。
⑦ $f(\theta)=a_1\cos{\theta}+a_2\cos{2\theta}+a_3\cos{3\theta}+\cdots+b_1\sin{\theta}+b_2\sin{2\theta}+b_3\sin{3\theta}+\cdots+C$
$(Cは定数)$
📜📜📜
ここで⑦の両辺に$\cos{\theta}$をかけて、$-\pi$から$\pi$で積分すると、
⑧ $$\begin{eqnarray*}\int_{-\pi}^{\pi} f(\theta)\cos{\theta}\, d\theta=\int_{-\pi}^{\pi}a_1\cos{\theta}\cos{\theta}\, d\theta+\int_{-\pi}^{\pi}a_2\cos{2\theta}\cos{\theta}\, d\theta+\int_{-\pi}^{\pi}a_3\cos{3\theta}\cos{\theta}\, d\theta+\cdots\\\\+\int_{-\pi}^{\pi}b_1\sin{\theta}\cos{\theta}\, d\theta+\int_{-\pi}^{\pi}b_2\sin{2\theta}\cos{\theta}\, d\theta+\int_{-\pi}^{\pi}b_3\sin{3\theta}\cos{\theta}\, d\theta+\cdots+C\int_{-\pi}^{\pi}\cos{\theta}\, d\theta\end{eqnarray*}$$
さて、ここで、
$ \int_{-\pi}^{\pi}\sin{m\theta}\cos{n\theta}\, d\theta=0 $
になります。
その理由はsin関数は奇関数だからです。
奇関数とは、原点に中心にして点対称になる関数で、以下のように
$ \int_{-L}^{L}\sin{\theta}\, d\theta=0 $
になります。
ここで、奇関数×偶関数=奇関数になります。
そしてcos関数は偶関数です。
つまり、
$ \int_{-\pi}^{\pi}\sin{m\theta}\cos{n\theta}\, d\theta $
は奇関数になるため、0になるという訳です。
よって、
⑧の
$\int_{-\pi}^{\pi}b_1\sin{\theta}\cos{\theta}\, d\theta+\int_{-\pi}^{\pi}b_2\sin{2\theta}\cos{\theta}\, d\theta+\int_{-\pi}^{\pi}b_3\sin{3\theta}\cos{\theta}\, d\theta\cdots$
の部分は全て0になります。
さらに、
$ \frac{1}{\pi} \int_{-\pi}^{\pi}\cos{m\theta}\cos{n\theta}\, d\theta = \delta_{mn}$
というクロネネッカーのデルタと呼ばれる$\delta_{mn}$が成り立ち、$m=n$の時、$\delta_{mn}=1$となり、$m\neq n$の時、$\delta_{mn}=0$となります。
(すみませんがここでは証明は割愛)
このため、⑧の$a$がついている項の2項目以降は全て0になります。
よって、⑧は以下のように書けます。
$ \int_{-\pi}^{\pi} f(\theta)\cos{\theta}\, d\theta=\int_{-\pi}^{\pi}a_1\cos{\theta}\cos{\theta}\, d\theta $
さらにクロネネッカーのデルタより、$m=n$の時、$\delta_{mn}=1$となるので、
$ \int_{-\pi}^{\pi} f(\theta)\cos{\theta}\, d\theta=a_1\pi $
ここまでは⑦の式の両辺に$\cos{\theta}$をかけて、$-\pi$から$\pi$で積分した場合を考えました。
📜📜📜
で、
$$ a_1 = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{\theta}\, d\theta $$
となります。
同じ要領で今度は⑦の式の両辺に$\cos{2\theta}$をかけて$-\pi$から$\pi$で積分した場合を考えます。
そうすると、上記と同様に計算ができて、
$$ a_2 = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{2\theta}\, d\theta $$
が求まります。よって$n$の時は、
⑨$$ a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{n\theta}\, d\theta $$
となります。
また、$a_0$は$\cos{0}=1$なので
⑩$$ a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\, d\theta $$
となります。
📜📜📜
⑦の式の両辺にsinをかけて$-\pi$から$\pi$で積分した場合、今度はsinの項が残ることになります。
よって同様に計算していくと、
⑪$$ b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\sin{n\theta}\, d\theta $$
が求まります。
📜📜📜
最後に、⑦の両辺を単純に$-\pi$から$\pi$で積分した場合は、
$$\begin{eqnarray}\int_{-\pi}^{\pi} f(\theta)\, d\theta=\int_{-\pi}^{\pi}a_1\cos{\theta}\, d\theta+\int_{-\pi}^{\pi}a_2\cos{2\theta}\, d\theta+\int_{-\pi}^{\pi}a_3\cos{3\theta}\, d\theta+\cdots\\+\int_{-\pi}^{\pi}b_1\sin{\theta}\, d\theta+\int_{-\pi}^{\pi}b_2\sin{2\theta}\, d\theta+\int_{-\pi}^{\pi}b_3\sin{3\theta}\, d\theta+\cdots+C\int_{-\pi}^{\pi}\, d\theta\end{eqnarray}$$
となる訳だけど、
$\int_{-\pi}^{\pi}\cos{n\theta}\, d\theta$ も $\int_{-\pi}^{\pi}\sin{n\theta}\, d\theta$ も0になるから、残るのは、
$C\int_{-\pi}^{\pi}\, d\theta$ だけになって、結局、
$$ \int_{-\pi}^{\pi} f(\theta)\, d\theta=C\int_{-\pi}^{\pi}\, d\theta = 2C\pi$$
となり、$C$は
$$ C = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(\theta)\, d\theta $$
と表されます。
⑩より、
$$ a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\, d\theta $$
なので、
$$ C = \frac{a_0}{2} $$
と表すことができます。
ここまでをまとめると、⑦の式は、
$$C + \sum_{n=1}^{\infty} (a_n\cos{n\theta} + b_n\sin{n\theta})$$
と表すことができるので、
⑫ $$\frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n\cos{n\theta} + b_n\sin{n\theta})$$
となります。
そして、この式の$a_n$と$b_n$は上記より⑩と⑪の式になります。
ここまでがフーリエ級数の式です。
つまり、この⑩、⑪、⑫の式がフーリエ級数の式です。
もう一度以下にまとめます。
$$ a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{n\theta}\, d\theta $$
$$ a_0 = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\, d\theta $$
$$\frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n\cos{n\theta} + b_n\sin{n\theta})$$
複素形式への拡張
ここまではsinとcosを使った式でした。
上記でオイラーの公式に触れた時もそうですが、複素数を使うと、sinとcosは指数関数eに置き換えられます。
それをこれから求めていきましょう。
上記でも書いたようにオイラーの公式は、$e^{i\theta}=\cos{\theta}+i\sin{\theta}$であり、
$e^{in\theta}=\cos{n\theta}+i\sin{n\theta}$とも書けます。よって、
$$ \cos{n\theta}=\frac{e^{in\theta}+e^{-in\theta}}{2} $$
$$\sin{n\theta}=\frac{e^{in\theta}-e^{-in\theta}}{2 i} $$
となります。よって、⑫の式は以下のように変形できる。以下の式では$\frac{1}{i}=\frac{i}{i^2}=-i$も使っています。
⑬$$\begin{eqnarray}\frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n\cos{n\theta} + b_n\sin{n\theta}) = \frac{a_0}{2} + \sum_{n=1}^{\infty} (a_n\frac{e^{in\theta}+e^{-in\theta}}{2} + b_n\frac{e^{in\theta}+e^{-in\theta}}{2i}) \\\\ = \frac{a_0}{2} + \sum_{n=1}^{\infty} (\frac{a_n-ib_n}{2}e^{in\theta} + \frac{a_n-ib_n}{2}e^{-in\theta})\end{eqnarray}$$
この⑬の
$$ \frac{a_0}{2} + \sum_{n=1}^{\infty} (\frac{a_n-ib_n}{2}e^{in\theta} + \frac{a_n-ib_n}{2}e^{-in\theta}) $$
のシグマをとって順番に並び替えてみると、⑬は
$$ \cdots + \frac{a_2+ib_2}{2}e^{-i2\theta} + \frac{a_1+ib_1}{2}e^{-i\theta} + \frac{a_0}{2} + \frac{a_1-ib_1}{2}e^{i\theta}+\frac{a_2-ib_2}{2}e^{i2\theta} + \cdots $$
となります。
ここで、$cos{n\theta}=cos{(-n\theta)}$、$sin{n\theta}=-sin{(-n\theta)}$ である
これを
⑪と⑫の式に代入してみると
$$ a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{n\theta}\, d\theta = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{(-n\theta)}\, d\theta = a_{-n} $$
$$ b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\sin{n\theta}\, d\theta = -\frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\sin{(-n\theta)}\, d\theta = -b_{-n} $$
が求まります。
よって⑬はさらに、
$$ \cdots + \frac{a_{-2}-ib_{-2}}{2}e^{-i2\theta} + \frac{a_{-1}-ib_{-1}}{2}e^{-i\theta} + \frac{a_0}{2} + \frac{a_1-ib_1}{2}e^{i\theta}+\frac{a_2-ib_2}{2}e^{i2\theta} + \cdots $$
となります。この式は$c_{n} \equiv \frac{a_{n}-ib_{n}}{2}$とすると、
$$ f(\theta) = \sum_{n=\infty}^{\infty} c_ne^{in\theta} $$
と書けます。とても簡単にまとめられました。
$$c_n \equiv \frac{a_{n}-ib_{n}}{2}$$も書き換えると、
$$\begin{eqnarray}\frac{a_{n}-ib_{n}}{2} = \frac{\frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\cos{n\theta}\, d\theta-i\frac{1}{\pi}\int_{-\pi}^{\pi} f(\theta)\sin{n\theta}\, d\theta}{2} \\\\ = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(\theta){\cos{(-n\theta)+i\sin{(-n\theta)}}}\, d\theta \\\\ = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(\theta)e^{-in\theta}\, d\theta\end{eqnarray}$$
ここまでで複素形式に変形できました。
まとめると、以下のようになり、これで複素形式への変換が完了しました。
$$ f(\theta) = \sum_{n=\infty}^{\infty} c_ne^{in\theta} $$
$$ c_{n}= \frac{1}{2\pi}\int_{-\pi}^{\pi} f(\theta)e^{-in\theta}\, d\theta $$
最後に
式の番号⑤を抜かしていました。すみません。
今回、フーリエ級数展開を複素数を使う式にまで求めることができました。
フーリエ変換への理解を進められたので嬉しいです。