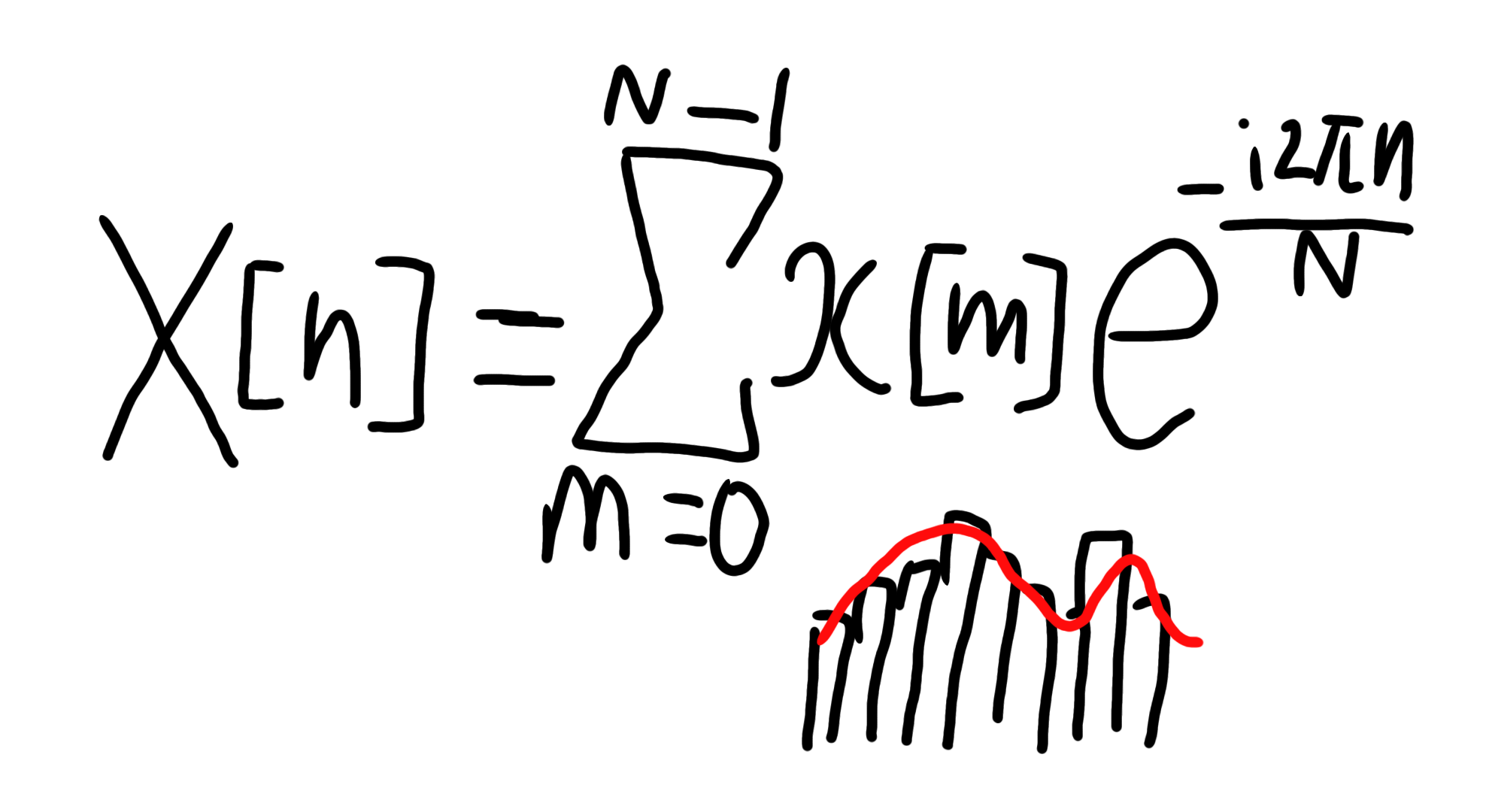はじめに
フーリエ変換をデジタルで扱う時、困る事としては、フーリエ変換は連続な関数に使用するという事です。
しかし、デジタルの世界では値はとびとびの値になります。
そこでデジタルの世界で使えるように離散の値を用いた離散フーリエ変換が登場します。
今回は、離散フーリエ変換を求めてみようと思います。
前回はフーリエ変換の式まで求めました。
前回の記事👇
ただ、離散フーリエ変換を求めるアプローチは
フーリエ級数展開⇒離散フーリエ変換
という流れになります。
フーリエ級数展開を求めた時の記事は以下👇
こちらの記事で求めた、フーリエ級数展開の式を見てみましょう。
$$ c_n = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(\theta)e^{-in\theta}\, d\theta $$
$$ f(\theta) = \sum_{n=\infty}^{\infty} c_ne^{in\theta} $$
こちらの式を使うことになります。
フーリエ級数とフーリエ変換と離散フーリエ変換について表にまとめると以下のようになります。
| データの周期性 | 連続かどうか | 周波数 | |
|---|---|---|---|
| フーリエ級数展開 | 周期的 | 連続 | とびとび |
| フーリエ変換 | 非周期的 | 連続 | 連続 |
| 離散フーリエ変換 | 非周期的 | 離散的 | とびとび |
フーリエ級数展開⇒離散フーリエ変換
まず、少し時間tで式を変換してみます。
$\theta=\frac{2 \pi}{T} t \quad \Longleftrightarrow \quad d \theta=\frac{2 \pi}{T} d t .$とおくと、
- $ t=0 ⇒ \theta=0 $
- $ t=T ⇒ \theta=2\pi $
となります。
これは、時間$t$がちょうど1周期$T$進むと、角度 $\theta$ は $2\pi$ 回転する という対応関係を表しています。
これを使うと、$c_n$は以下のように変換できます。
$$\begin{aligned}
c_n & =\frac{1}{2 \pi} \int_{-\pi}^\pi f(\theta) e^{-i n \theta} d \theta \\\\
& =\frac{1}{2 \pi} \int_{0}^{T} f\left(\frac{2 \pi}{T} t\right) e^{-i n \frac{2 \pi}{T} t} \frac{2 \pi}{T} d t \\\\
& =\frac{1}{T} \int_{0}^{T} f\left(\frac{2 \pi}{T} t\right) e^{-i \frac{2 \pi n}{T} t} d t
\end{aligned}$$
この積分範囲だけど$[0,2\pi]$でも $[−\pi,\pi]$でも結局同じ意味なので、$T$に変えた時に$[0,T]$になっています。
$f\left(\frac{2 \pi}{T} t\right)$については、
$$f\left(\frac{2 \pi}{T} t\right)=\sum_{n=-\infty}^{\infty} c_n e^{i n \frac{2 \pi}{T} t}=\sum_{n=-\infty}^{\infty} c_n e^{i \frac{2 \pi n}{T} t}$$
となります。
$$ g(t) = f\left(\frac{2 \pi}{T} t\right) $$
として整理すると、
$$ c_n =\frac{1}{T} \int_{0}^{T} g(t) e^{-i \frac{2 \pi n}{T} t} dt $$
になります。
ここで、以下の図をイメージします。
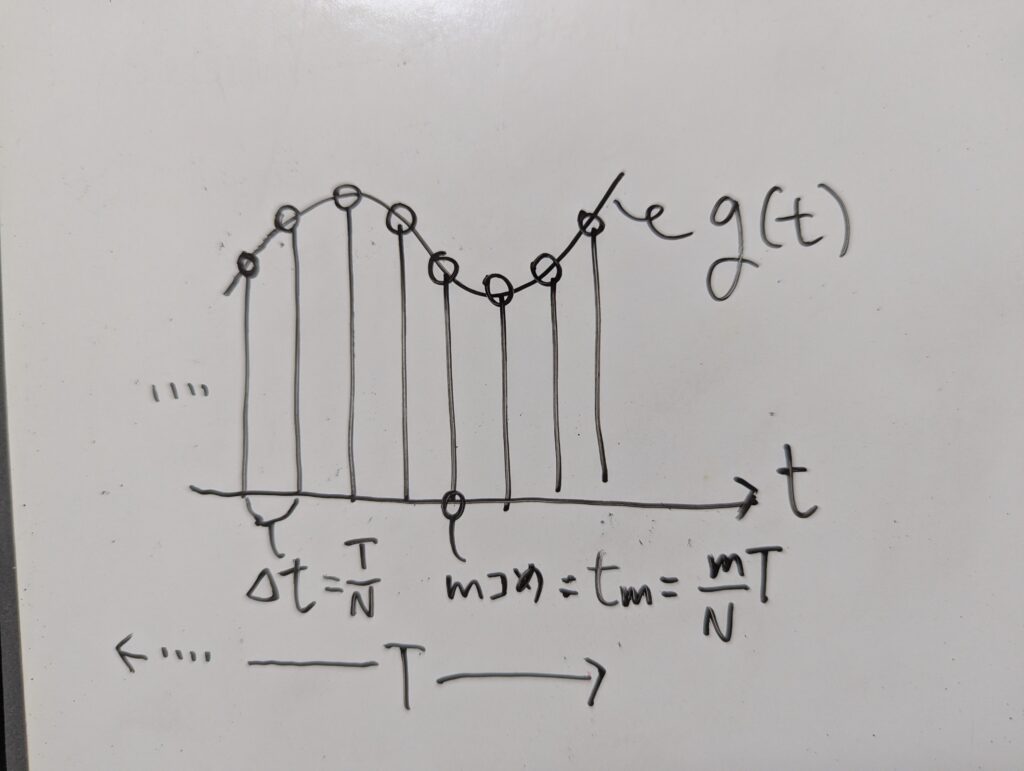
さて、実際の計算では有限個のデータしか扱えないので、周期を $T$、サンプル数を $N$ とすると、区間 $(0,T)$ 等間隔に $N$点サンプリングすることになります。
1区間の幅は
$$\Delta t=\frac{T}{N}$$
となります。
また、$m$個めの$t_m$は
$$ t_m=\frac{m T}{N}, \quad n=0,1, \ldots, N-1 $$
となります。
ここまでを上記のイメージ図のグラフに追記すると以下のようになります。
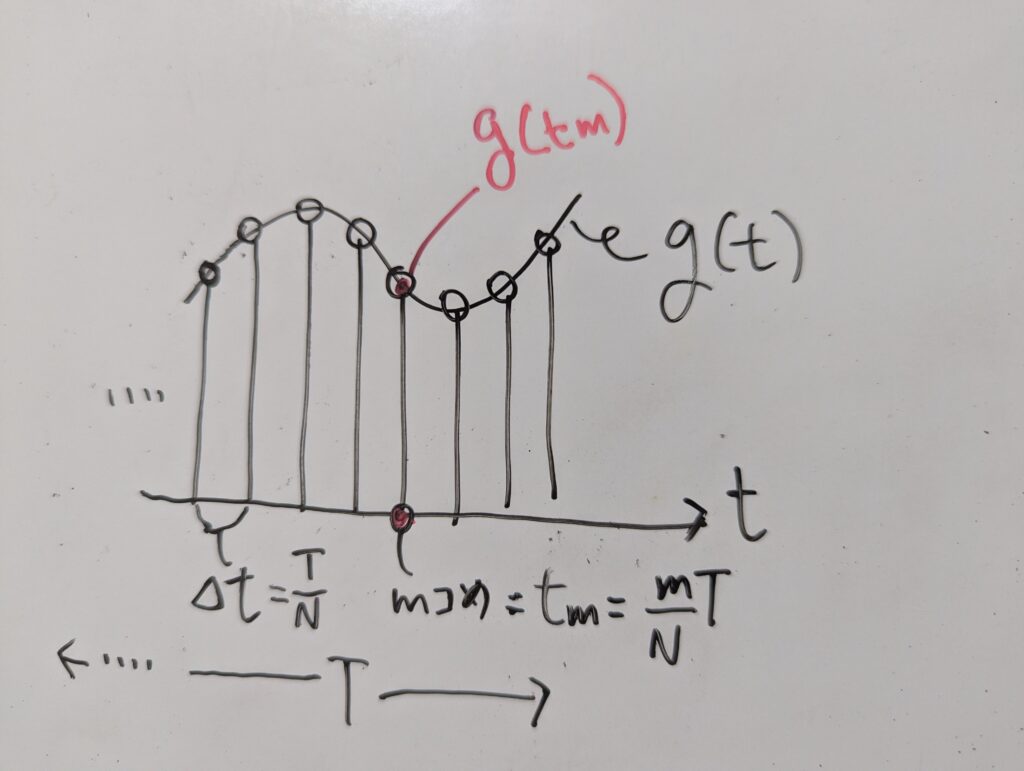
サンプルの値は$ x[m]=g(t_m) = g(\frac{mT}{N})$です。
これもグラフに追記してみます。
フーリエ級数の積分は以下のようになります。
$$ c_n=\frac{1}{T} \int_0^T g(t) e^{-\frac{i 2 \pi n t}{T}} dt $$
積分の定義より
$$\int_0^T g(t) e^{-\frac{i 2 \pi k t }{T}} d t \approx \sum_{m=0}^{N-1} g\left(t_n\right) e^{-\frac{i 2 \pi k t_{m}}{T}} \Delta t = \sum_{m=0}^{N-1} x[m] e^{-\frac{i 2 \pi m n}{N}} \frac{T}{N}$$
よって$c_n$は
$$ c_n \approx \frac{1}{T} \sum_{m=0}^{N-1} x[m] e^{-\frac{i 2 \pi m n}{N}} \frac{T}{N} = \frac{1}{N} \sum_{m=0}^{N-1} x[m] e^{-\frac{i 2 \pi m n}{N}} $$
となります。
これで離散フーリエ変換を求めることができました。
次に実際に離散フーリエ変換をプログラムで試していこうと思うのですが、今のままだと計算量が$O(N^2)$になってしまい、たくさん計算しなければなりません。
そこで、FFT(fast Fourier transform / 高速フーリエ変換)というアルゴリズムを使います。
FFTについて
FFTを使うと計算量が$O(N^2)$から$O(N\log{N})$へと改善できます。
$$\frac{1}{N} \sum_{m=0}^{N-1} x[m] e^{-\frac{i 2 \pi m n}{N}}$$
をいかに効率よくとくかを考えます。
$\frac{1}{N}$は計算量には関係ないので、
$$ X[n] = \sum_{m=0}^{N-1} x[m] e^{-\frac{i 2 \pi m n}{N}} $$
とおいて、この$X[n]$を効率よく解きます。
普通に解くと、
- $n$(周波数インデックス)を0からN-1個計算する必要がある⇒つまり出力がN個ある。
- 各$c_n$をそれぞれ計算するとなると、入力の全サンプル$x[m]$ ($m=0,\dots,N-1$)を使って和をとる
- よって$N^2$ の計算量になる。
- 出力 $X[0]$ を求めるとき:N 個の積和
- 出力 $X[1]$ を求めるとき:N 個の積和
- …
- 出力 $X[N−1]$ を求めるとき:N 個の積和
で、$N^2$ の計算量になるって感じです。
FFTは偶数番目と奇数番目に分けて離散フーリエ変換をしていく流れになります。
例えば、入力データが8個の場合、
$$x = [x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7]$$
DFT の計算式は以下のようになります。
$$X[n]=\sum_{m=0}^7 x[m] e^{-i 2 \pi m n / 8}, \quad n=0, \ldots, 7$$
これを愚直に計算すると 8×8=64 回の計算が必要です。
つまり8の2乗ですね。
ここで、偶数番目と奇数番目にわけて、それぞれに対してDFTを行う処理を繰り返します。
今回の場合は1回目の分割で、
- 偶数番目:$x[0],x[2],x[4],x[6]$⇒DFTをして$E$(長さ4)が求まる
- 奇数番目:$x[1],x[3],x[5],x[7]$⇒DFTをして$O$(長さ4)が求まる
元々は「8点のDFT」だったけど、これで「2つの4点のDFT」になります。
2回目の分割では、それぞれの長さ4のDFTをさらに分割します:
- $E$ は「偶数偶数」「偶数奇数」に分割(それぞれ長さ 2)
- $O$ も同様に分割(それぞれ長さ 2)
この時点で4つの長さ2のDFTになります。
3回目の分割も同様の処理をしていきます。
「長さ2のDFT」は「長さ1のDFT×2」に分割できます。
長さ1の DFT は「ただのコピー」なのでここで分割終了。
このようにすることで計算量が$O(N\log{N})$になります。
と、ここまでつらつらと書きましたが、実際にFFTをするときはpythonではライブラリが用意されているだけなので、簡単に済みます。
最後に
今回は、フーリエ変換では連続な関数にしか使えないことから、離散フーリエ変換を求めてみました。
さらにFFTも言及してみました。
次回以降でpythonを使った実践をしてきたいと思います。