覚えたくない数学 （三角関数）

はじめに

「数学では暗記はしないように」とはよく言われることです。

しかし、実際数学に挑むと公式がいくつも出てきて、それぞれを理解することに屈して、暗記する道を選びがちです。

その道の先は数学の挫折に繋がります。

そんなことが起きないように、数学をロジカルに解いていける練習をするために、問題を解くときの武器とするために、数学で暗記しがちな数式をできるだけ覚えないようにするのが、この「覚えない数学」です。

今回は三角関数を取り上げます。

三角関数の公式は結構あるため、暗記しがちです。

先に結論から

先に結論から言うと、咲いたコスモスは覚えた方がいいです。

その理由は、テストの度に毎回導出するのは時間が足りなるからです。

じゃあ、なんで証明をするのか、導出をしてみる必要があるのかと言うと、訳も分からず咲いたコスモスを使うのと、三角関数の仕組みを知ったうえで咲いたコスモスを使うのでは全然違うと思うからです。

だから、一回、自分のノートに書きだしたりして、自分の頭の中で咀嚼することが大切です。

三角関数の公式

三角関数の基本を軽く記載します。

以下のような単位円上の点を考えます。

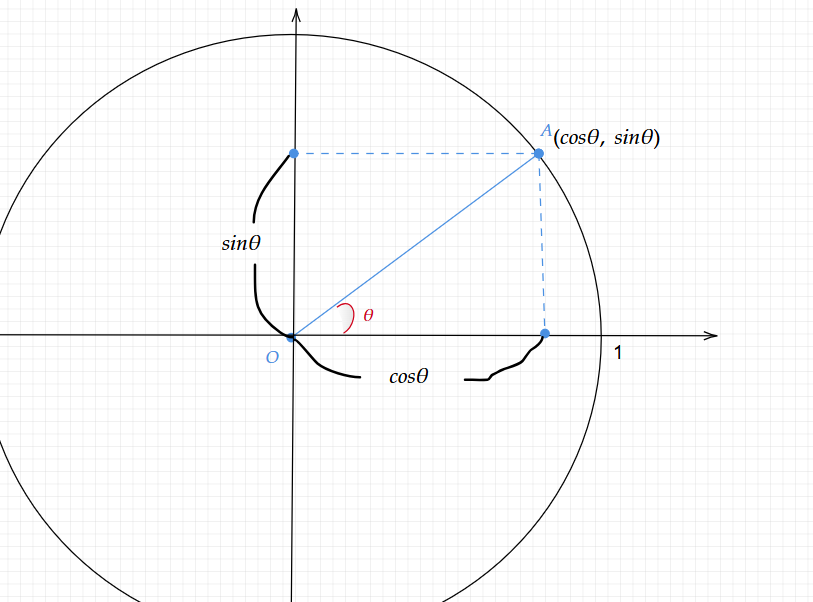
点Aの座標は$(\cos \theta ,\ \sin \theta )$です。

これが意味することは以下のことです。

単位円なので$\cos \theta$ はOAの長さが1であり、これにより上記三角形における$\cos \theta$ の定義からAから垂直にx軸に降ろした点の原点からの距離は$\cos \theta(=1\times \cos \theta)$となります。

点Aからy軸に垂直に降ろした点の原点からの距離も同様に$\sin \theta$となります。

三角関数の基本をより詳しく知りたければ、数学ガールの三角関数編がオススメです。

さて、まず、三角関数の公式を書きならべてみます。

加法定理

まずは一番最初に触れる加法定理です。

三角関数と言えばこの公式で、咲いたコスモスとかで覚える公式です。

和積の式

次に和積の式です。

そのままの名前で、和⇒積になる式です。

積和の式

積和の式です。

これもそのまま積⇒和になる式です。

2倍角の式

最後に2倍角の式です。

2倍の角がどのような値になるかを示す式です。

ここまで見ると、かなり多くの式がありますね。

証明していく

上記の式を証明していきます。

まず、単位円に以下のような三角形を作っていきます。

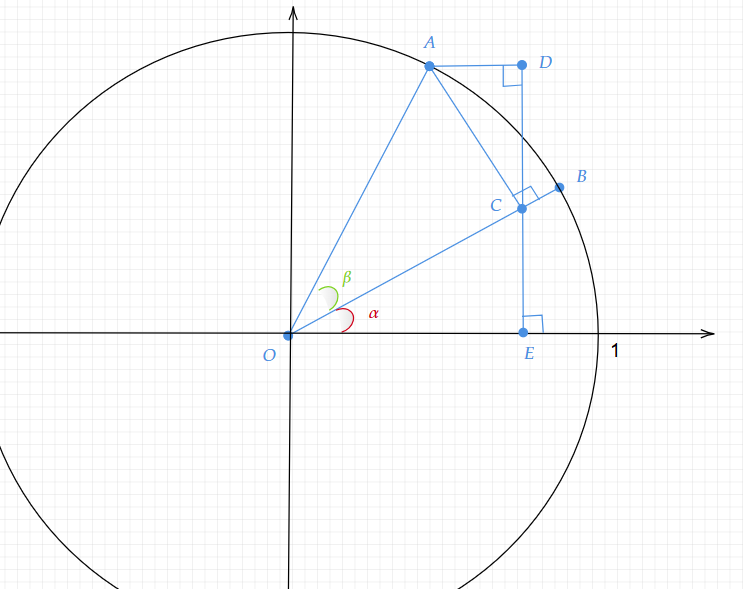
• AとBはそれぞれ、Bが角度$\alpha$ 分の点、そして更に角度を$\beta$分付ける点をAとする
• OAからOBへ垂直に線を降ろして、交わる点をCとする
• 点Cからx軸に垂直に降ろした点はEとし、その直線に点Aから垂直に交わる点をDとする

ここで作った三角形に以下のように更に補助線を引きます。

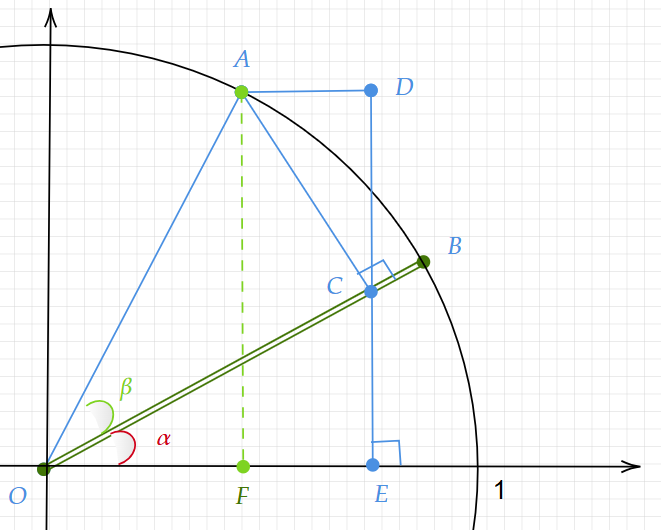
点Aからx軸に垂直に線を降ろし、その点をFとします。

OAの長さは1なので、OFは$\displaystyle cos( \alpha +\beta )$になります。

OCは三角形OACでみると、OAが1であることにより、$\cos\beta$になります。

さらにOCの長さが決まるという事はOEも求まることになる。$\cos\beta$のさらに$\cos\alpha$倍なので、$\cos\beta cos\alpha$となります。

さて、ここで、∠DCAは$\alpha$です。

なぜなら、∠OCEを$\gamma$とすると、∠DCAはED上の点Cに着目すると、$180° – 90° -\gamma =90° -\ \gamma$であり、三角形OECに着目すると、$\alpha =180° -90° -\gamma =90° -\ \gamma$だからです。

よって、以下の画像のようになります。

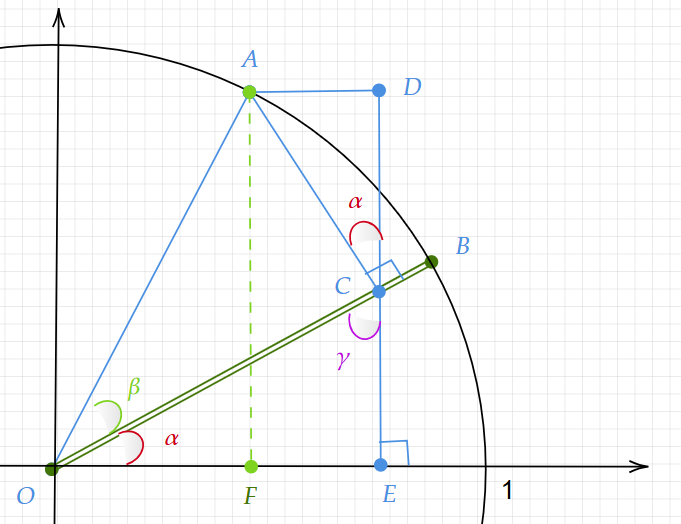
ACは$\sin \beta$になります。

この後、三角形ACDで見ると、ACが決まって$\sin \beta$となり、∠DCAも$\alpha$と分かっているので、ADが$\sin \beta \sin \alpha$となります。

AD=FEで$FE=\sin \beta \sin \alpha$となります。

OFは三角形OAFを考えると、$OF=\cos( \alpha +\beta )$でOE=OF+FEとなりこれで材料は整いました。

$\cos \beta \cos \alpha =\cos( \alpha +\beta ) +\sin \beta \sin \alpha$

この式を変更すると、$\cos( \alpha +\beta ) =\cos \beta \cos \alpha -\sin \beta \sin \alpha$となります。

$\cos( \alpha +\beta )$が出てきましたね。

さてここで以下の図を考える

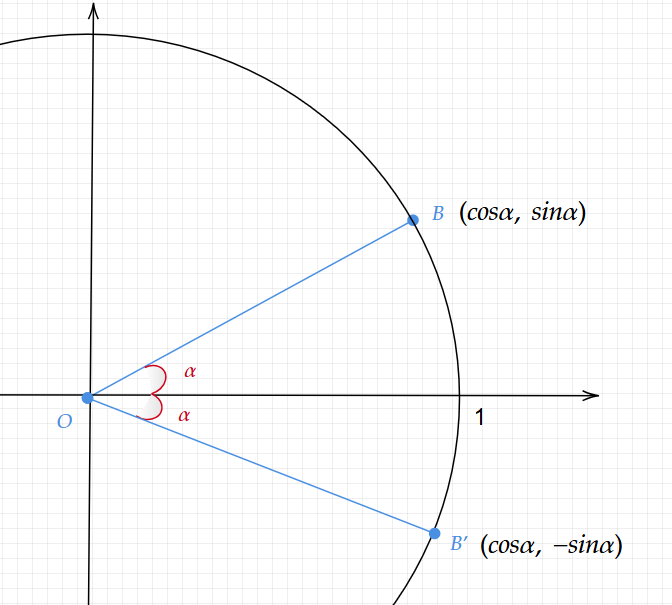
$\alpha$の角度分反対側にした単位円上の点をA’とします。

この時、$-\alpha$となります。

そして、その時の点の座標は$(\cos\alpha, -\sin\alpha)$となります。

よって、$(\cos(-\alpha), \sin(-\alpha))=(\cos\alpha, -\sin\alpha)$となります。

ここで、$\cos( \alpha – \beta )$を考えた時、$\cos( \alpha + (-\beta) )$とも考えられます。

$\cos( \alpha +\beta ) =\cos \beta \cos \alpha -\sin \beta \sin \alpha$は上記で求めたので、これを使うと、$\cos( \alpha + (-\beta) ) = \cos (-\beta) \cos \alpha -\sin (-\beta) \sin \alpha = \cos \beta \cos \alpha + \sin \beta \sin \alpha$となり、2つ目の式、$\cos( \alpha – \beta ) = \cos \beta \cos \alpha + \sin \beta \sin \alpha$が求まることになります。

次にsinの式を考えます。

さて再度以下の図を考えてみます。

AEは$\sin (\alpha + \beta)$であることがわかります。

つまり、DEも$\sin (\alpha + \beta)$になります。

上記で、ACは$\sin \beta$と決まっていて、∠ACDも$\alpha$と分かっているので、CDは$\sin \beta \cos \alpha$となります。

CEはOCが$\cos\beta$であるから、三角形OCEでみると、$\cos\beta \sin\alpha$となります。

よって、DE=AC+CEとなり、$\sin (\alpha + \beta)=\sin \beta \cos \alpha + \cos\beta \sin\alpha=\sin\alpha\cos\beta+\cos \alpha\sin \beta$が導けます。

これが求まれば、また$\sin (\alpha + (-\beta))=\sin\alpha\cos\beta-\cos \alpha\sin \beta$
と求められます。

ここまでで、

①

$$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$$

②

$$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$$

③

$$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$$

④

$$\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta$$

が求められました。

加法定理ができるようになると、積和の公式、和積の公式、2倍角の公式が次々と求められようになります。

積和の公式を導く

① – ②を式変形すれば、

$$\cos \alpha \sin \beta = \frac{1}{2} \left[ \sin(\alpha + \beta) – \sin(\alpha – \beta) \right]$$

が求められます。

① + ②を式変形すれば、

$$\sin \alpha \cos \beta = \frac{1}{2} \left[ \sin(\alpha + \beta) + \sin(\alpha – \beta) \right]$$

が求められます。

同様に、

③ – ④の式変形で、

$$\sin \alpha \sin \beta = \frac{1}{2} \left[ \cos(\alpha – \beta) – \cos(\alpha + \beta) \right]$$

が、

③ + ④の式変形で、

$$\cos \alpha \cos \beta = \frac{1}{2} \left[ \cos(\alpha – \beta) + \cos(\alpha + \beta) \right]$$

が求まります。

和積の公式を求める

$\alpha =\frac{\alpha +\beta }{2} +\frac{\alpha -\beta }{2}$ 、 $\beta =\frac{\alpha +\beta }{2} +\frac{\alpha -\beta }{2}$ と書けます。

これは普通に書き方を変えただけです。

つまり $\displaystyle \sin \alpha =\sin\left(\frac{\alpha +\beta }{2} +\frac{\alpha -\beta }{2}\right)$と書けるわけで、$\displaystyle \sin \beta =\sin\left(\frac{\alpha +\beta }{2} -\frac{\alpha -\beta }{2}\right)$とも書けます。

また加法定理を使って$\displaystyle \sin( X+Y) +\sin( X-Y)$を整理すると、$\displaystyle \sin( X+Y) +\sin( X-Y) =2\sin X\cos Y$、、、⑤となります。

ここで$\displaystyle X=\frac{\alpha +\beta }{2}$、$\displaystyle Y=\frac{\alpha -\beta }{2}$と置くと⑤は$\displaystyle \sin \alpha \ +\ \sin \beta \ =\ 2\sin\left(\frac{\alpha +\beta }{2}\right)\cos\left(\frac{\alpha -\beta }{2}\right)$が導けます。

同様に考えると、$\displaystyle \sin( X+Y) \ -\ \sin( X-Y) =2\cos X\sin Y$なので、これも$\displaystyle X=\frac{\alpha +\beta }{2}$、$\displaystyle Y=\frac{\alpha -\beta }{2}$を代入して、$\displaystyle \sin \alpha \ -\ \sin \beta =2\cos\left(\frac{\alpha +\beta }{2}\right)\sin\left(\frac{\alpha -\beta }{2}\right)$が導けます。

同様に、$\displaystyle \cos( X+Y) +\cos( X-Y)$からは

$\displaystyle \cos \alpha \ +\ \cos \beta \ =\ 2\cos\left(\frac{\alpha +\beta }{2}\right)\cos\left(\frac{\alpha -\beta }{2}\right)$

は求まるし、

$\displaystyle \cos( X+Y) -\cos( X-Y)$からは

$\displaystyle \cos \alpha \ -\ \cos \beta \ =\ 2\sin\left(\frac{\alpha +\beta }{2}\right)\sin\left(\frac{\alpha -\beta }{2}\right)$

が求まる。

2倍角の公式を求める

2倍角の公式も加法定理が求められていれば求められます。

$\sin(a + b)$で$a=b=\beta$のとき、加法定理で解いていくと、$\sin 2\beta = 2 \sin \beta \cos \beta$が導き出せるし、$\cos(a + b)$で$a=b=\beta$のとき、加法定理で解いていくと、$\cos 2\beta = \cos^2 \beta – \sin^2 \beta = 2\cos^2 \beta – 1 = 1 – 2\sin^2 \beta$が導き出せます。

そして、ここまでくれば、$\tan2\beta$も求められます。

$\displaystyle \tan2\beta=\frac{\sin2\beta}{\cos2\beta}=\frac{2\ \sin \ \beta \ \cos \ \beta }{\cos^{2} \beta -\sin^{2} \beta }$

で、分母分子を$\displaystyle \cos^{2} \beta$で割ると、

$\displaystyle \tan 2\beta \ =\frac{2\tan \beta }{1-\tan^{2} \beta }$

となり、2倍角の公式も求められます。

最後に

この記事書くのにめっちゃ大変でした、、、、。