はじめに
前回、離散フーリエ変換の式を求めてみました。
今回は離散フーリエ変換をpythonで実践したいと思います。
音声データ⇒離散フーリエ変換⇒振幅
フーリエ変換は時間領域の値を周波数領域(横軸を周波数、縦軸を振幅としたもの)に変換する手法です。
時間領域の値は音の波形で表されます。
波形は、横軸:時間(seconds)、縦軸:振幅(Amplitude)です。
今回使う音声データは以下のサイトから取ってきました。
「猫の鳴き声1」の「ニャー」という鳴き声のデータです。
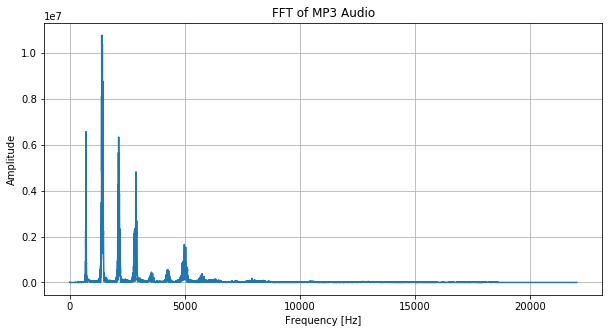
この猫の鳴き声をフーリエ変換にかけると以下のようなグラフになります。
縦軸が振幅で、横軸が周波数です。
pythonコードは以下のように簡単にフーリエ変換できます。
from pydub import AudioSegment
import numpy as np
import matplotlib.pyplot as plt
# 1. mp3ファイルを読み込み
sound = AudioSegment.from_mp3("./data/猫の鳴き声1.mp3").set_channels(1)
# 2. 音声データをnumpy配列に変換
samples = np.array(sound.get_array_of_samples())
fs = sound.frame_rate
# 3. FFTを実行
N = len(samples)
fft_result = np.fft.fft(samples)
freq = np.fft.fftfreq(N, d=1/fs)スペクトログラム
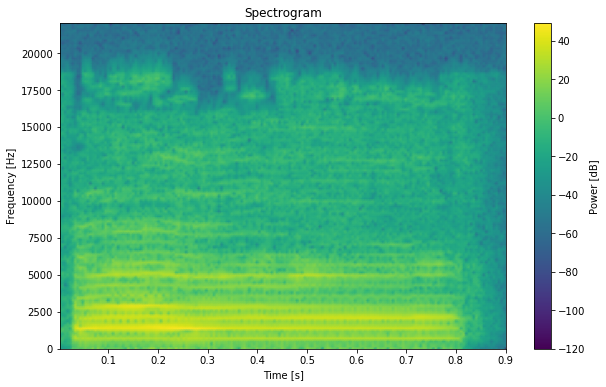
次にスペクトログラムを求めてみます。
上記ではフーリエ変換を用いて音声波形を周波数成分に分解しました。
この分解したものはスペクトルというのですが、スペクトルが時間方向に並んだものがスペクトログラムです。
フーリエ変換を施すと時間の情報がなくなってしまうので、短時間フーリエ変換を使用することで、時間の情報を付与します。
コードは以下のようになります。
from pydub import AudioSegment
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import spectrogram
# MP3ファイルを読み込み(モノラルに変換)
sound = AudioSegment.from_mp3("./data/猫の鳴き声1.mp3").set_channels(1)
# numpy配列に変換
data = np.array(sound.get_array_of_samples())
rate = sound.frame_rate
# スペクトログラムを計算
f, t, Sxx = spectrogram(data, fs=rate)グラフとして表示すると以下のようになります。
声紋比較
さて、このスペクトログラムを使用して、今度は声紋比較を行ってみます。
声紋は音声を周波数分析した結果をスペクトログラムで表したもので、個人によって異なり、犯罪捜査などにも利用されているのだとか。
今回は上記でも使用した「猫の鳴き声1」の「ニャー」と言う音声と、「猫の鳴き声2」の「甘え声」というデータを比較して見ます。
まずはコードは以下のようになりました。
from pydub import AudioSegment
import numpy as np
from scipy.signal import stft
from scipy.fftpack import dct
from sklearn.metrics.pairwise import cosine_similarity
import matplotlib.pyplot as plt
# ==== 共通関数:音声からMFCCを抽出 ====
def compute_mfcc(signal, sr, num_ceps=13, nfft=2048, nfilt=26):
frame_size = 0.025
frame_stride = 0.01
frame_length = int(round(frame_size * sr))
frame_step = int(round(frame_stride * sr))
signal_length = len(signal)
# frames という行列(フレーム数 × フレーム長)を作成
num_frames = int(np.ceil(float(np.abs(signal_length - frame_length)) / frame_step)) + 1
pad_signal_length = num_frames * frame_step + frame_length
z = np.zeros((pad_signal_length - signal_length))
pad_signal = np.append(signal, z)
indices = np.tile(np.arange(0, frame_length), (num_frames, 1)) + \
np.tile(np.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
# フレームの端で音がブツッと切れないように滑らかにする
frames = pad_signal[indices.astype(np.int32, copy=False)]
frames *= np.hamming(frame_length)
# フーリエ変換の実施
mag_frames = np.absolute(np.fft.rfft(frames, nfft))
pow_frames = ((1.0 / nfft) * ((mag_frames) ** 2))
# メル尺度 (Mel scale) に変換して、聴覚特性を模倣
low_freq_mel = 0
high_freq_mel = 2595 * np.log10(1 + (sr / 2) / 700)
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2)
hz_points = 700 * (10 ** (mel_points / 2595) - 1)
bin = np.floor((nfft + 1) * hz_points / sr)
fbank = np.zeros((nfilt, int(np.floor(nfft / 2 + 1))))
for m in range(1, nfilt + 1):
f_m_minus = int(bin[m - 1])
f_m = int(bin[m])
f_m_plus = int(bin[m + 1])
for k in range(f_m_minus, f_m):
fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1])
for k in range(f_m, f_m_plus):
fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m])
# メルスペクトログラムを計算
filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)
filter_banks = 20 * np.log10(filter_banks)
# DCTで相関のある特徴を圧縮して、13次元くらいのMFCC特徴量を得る
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, :num_ceps]
return mfcc
# ==== 音声ファイルを読み込み ====
def load_audio_to_mfcc(file_path):
sound = AudioSegment.from_mp3(file_path).set_channels(1)
y = np.array(sound.get_array_of_samples()).astype(float)
sr = sound.frame_rate
mfcc = compute_mfcc(y, sr)
return mfcc, sr
# ==== 2つの音声を比較 ====
mfcc1, sr1 = load_audio_to_mfcc("./data/猫の鳴き声1.mp3")
mfcc2, sr2 = load_audio_to_mfcc("./data/猫の鳴き声2.mp3")
# 各フレームのMFCCを平均化して特徴ベクトル化
mean1 = np.mean(mfcc1, axis=0).reshape(1, -1)
mean2 = np.mean(mfcc2, axis=0).reshape(1, -1)
# コサイン類似度で比較(1.0 = 完全一致)
similarity = cosine_similarity(mean1, mean2)[0][0]
match_rate = similarity * 100
print(f"🎙️ 声の一致率: {match_rate:.2f}%")
# 可視化(MFCCの違い)
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.imshow(mfcc1.T, aspect='auto', origin='lower', cmap='magma')
plt.title("Voice 1 MFCC")
plt.subplot(1, 2, 2)
plt.imshow(mfcc2.T, aspect='auto', origin='lower', cmap='magma')
plt.title("Voice 2 MFCC")
plt.tight_layout()
plt.show()
こちらのコードではスペクトログラムにしてからメルスケールへの対数変換を行い、MFCC(声の特徴ベクトル)というベクトルにします。
MFCCは、メルスケール上のスペクトログラムをさらに圧縮して、「声の形そのもの」を数値化します。
実際の結果が以下です。ネコの音声はかなり高い精度で一致しています。
🎙️ 声の一致率: 99.06%二つの音声のMFCCのグラフも載せておきます。

ちなみに、「犬の鳴き声4」の「ク~ン…」を使ってみて比較してみると、
🎙️ 声の一致率: 97.21%となり、犬の鳴き声ともかなり近い値になってしまいました...。
最後に
実際に手を動かしてみてアウトプットすると、フーリエ変換の使いどころの理解が深まりますね!



