はじめに
先日、「ぶつり学入門」という本を読んでいたら、以下のような一節が出てきました。
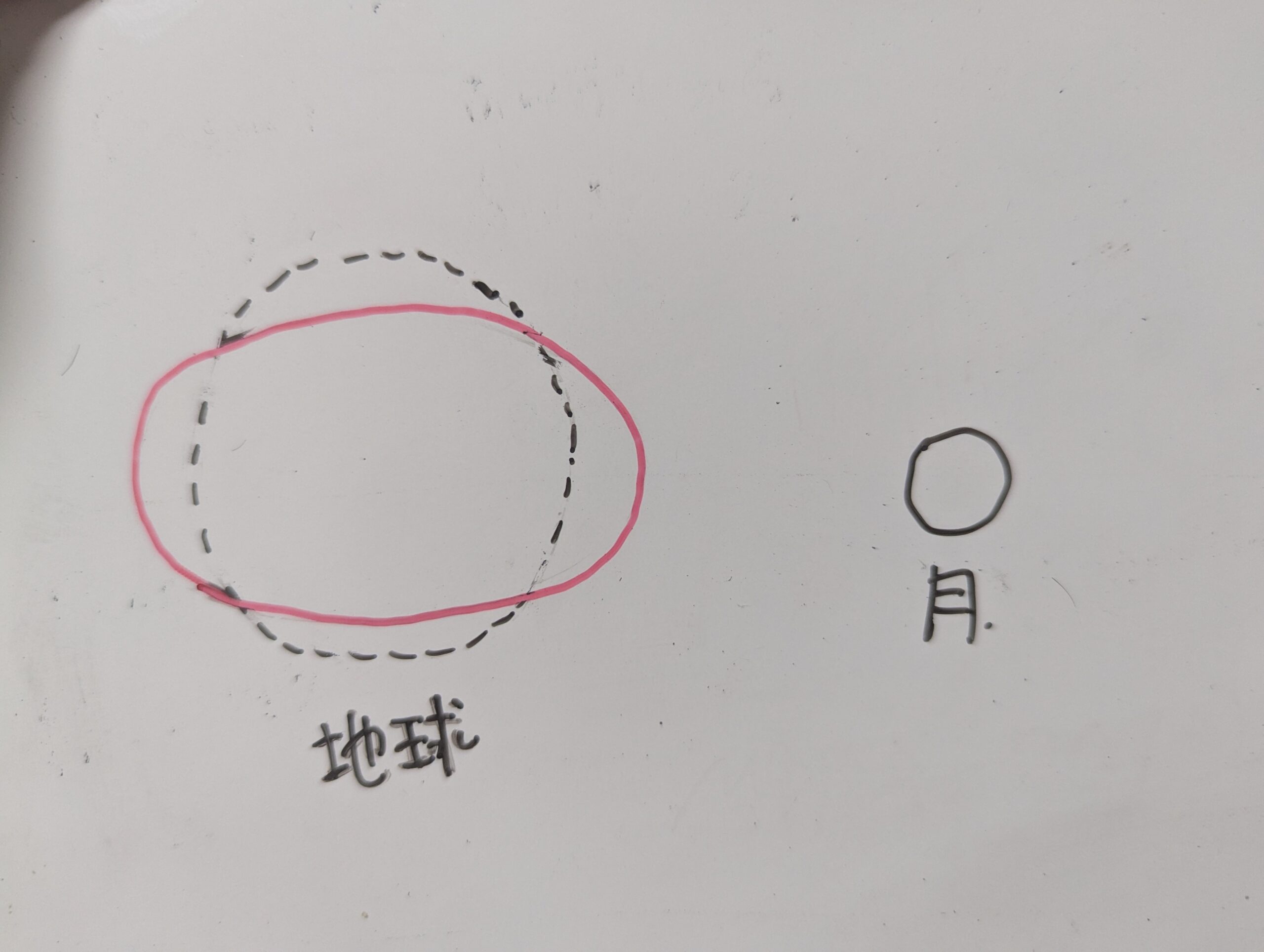
地球と月の間には「万有引力」と呼ばれる引き合う力が働いています。万有引力には、距離が近づくほど、大きくなるという特徴があります。そのため、地球の月に近い側で大きな万有引力を、それとは反対側ではより小さな万有引力を受けることになります。
そしてその結果地球は次のように変形しようとするのです。
「ぶつり学入門 物理学の視点で釣りを科学する」

「ぶつり学入門 物理学の視点で釣りを科学する」
??
「いや、万有引力が距離によって変わるものであるなら以下のような形になるのではないの?」と思いました。
なんでラグビー型やねん!って感じ。
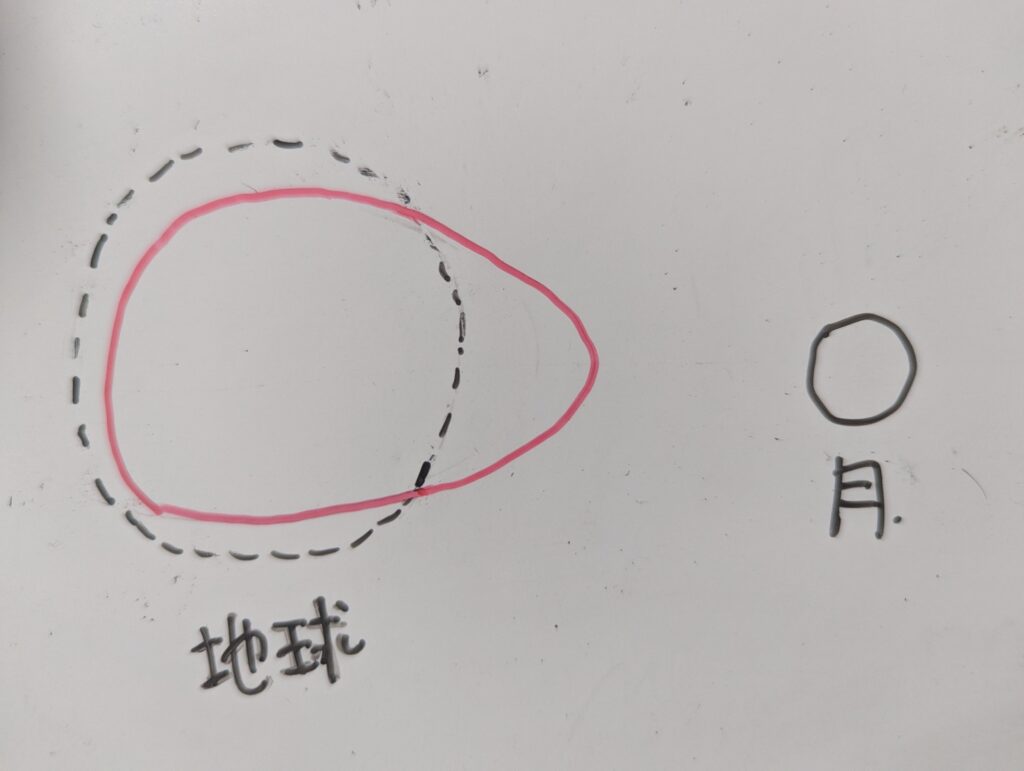
この図では月に近い側は引力が強くて、強く引っ張られるけど、月と反対側は引力が弱いのであまり引っ張られていないことを示しています。
本来ならこうなるんじゃないかな?って思って今回は自分で調べてみることにしました。
更に動機として潮の満ち引きが分かれば将来的に釣りの最適化に繋がるというコスパの目論見があったりします。
以下の記事を参考にさせていただきました。(結構難易度高めです。)
潮汐力
この、潮の満ち引きは潮汐力という力が影響しています。
潮汐力というのは月や太陽の重力が地球の異なる場所でわずかに異なることによって生まれる力です。
ラグビー型になるのはここに慣性の力が働くからです。
ひとまず潮汐力がラグビー型になる理由から求める
以下の図の状況を考えます。
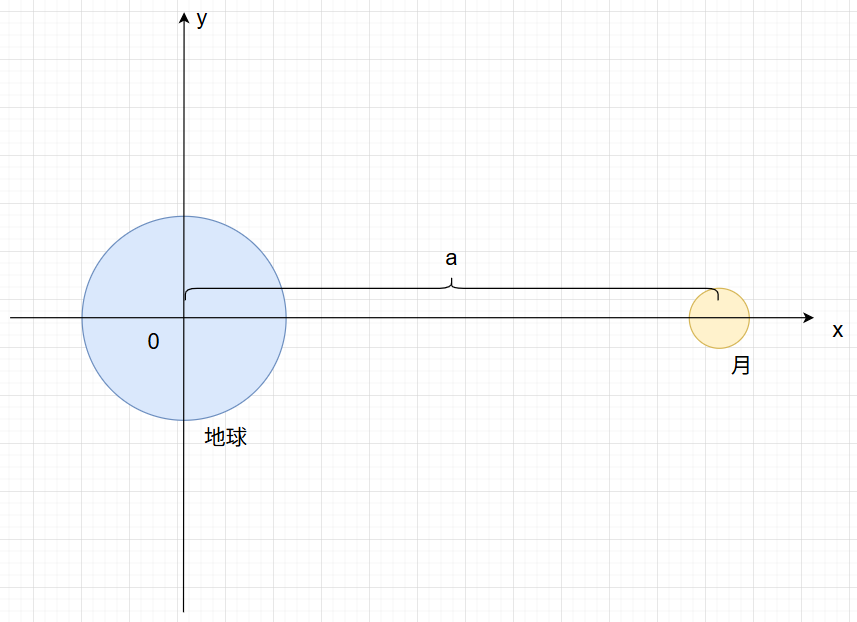
地球上のある点を考える
ここで、地球上のある点が月から受ける重力加速度は$m$を月の質量、$G$を万有引力定数とすると、
$$ \frac{G m}{(a-x)^2} $$
で表されます。(今回は図のように月に一番近い$(x, y, z) = (a, 0, 0)$の点で考えます)
一方で、地球自体は月から万有引力の力を受けます。
これは、
$$ \frac{G m M}{a^2} $$
で表されます。
ここで地球にはこの万有引力に対する慣性の力が働くことになります。
慣性の力は例えば、バスが急発進するとバスに乗っている乗客はその場にとどまろうとして後ろに引っ張られるような力が働きます。
地球にも同様の慣性力がかかっており、これを「並進慣性力」と呼びます。
そして、ここがポイントなんですけど、この慣性力、地球に一様にかかります。
つまり地球のどこの点でも同じ強さの力(並進慣性力)がかかることになります。
つまり以下のような感じ(オレンジのところは全て同じ強さの力)
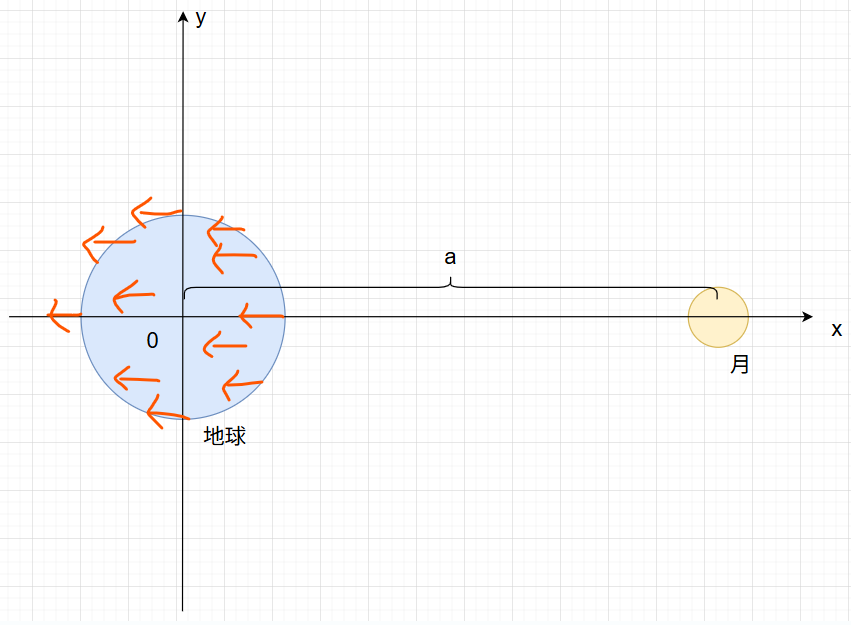
この一様な力は上記の万有引力の式と釣り合うので、加速度は
$$ \vec{F} = Ma_1 = \frac{G m M}{a^2} $$
$$ a_1 = \frac{G m }{a^2} $$
と求められます。これがどこの点でも同じ値になるという事です。
上記で記載の通り、月からの重力による加速度は$ \frac{G m}{(a-x)^2} $ですね。
この式は$x$に依存しています。
分母は$a-x$になっていて、月に近い方は分母が小さくなり、月に遠い方は分母が大きくなります。
その結果、$ \frac{G m}{(a-x)^2} $は月に近い方は大きくなり、月に遠い方は小さくなります。
$ \frac{G m }{a^2} $は一定ですので、$ \frac{G m}{(a-x)^2} $との差が生じます。
さらには図中の$y$軸のところは月に向かっていく矢印が斜めになるので、$y$方向にも加速度がかかりますね。
ここまでをまとめると、以下のような紫の矢印が現れます。
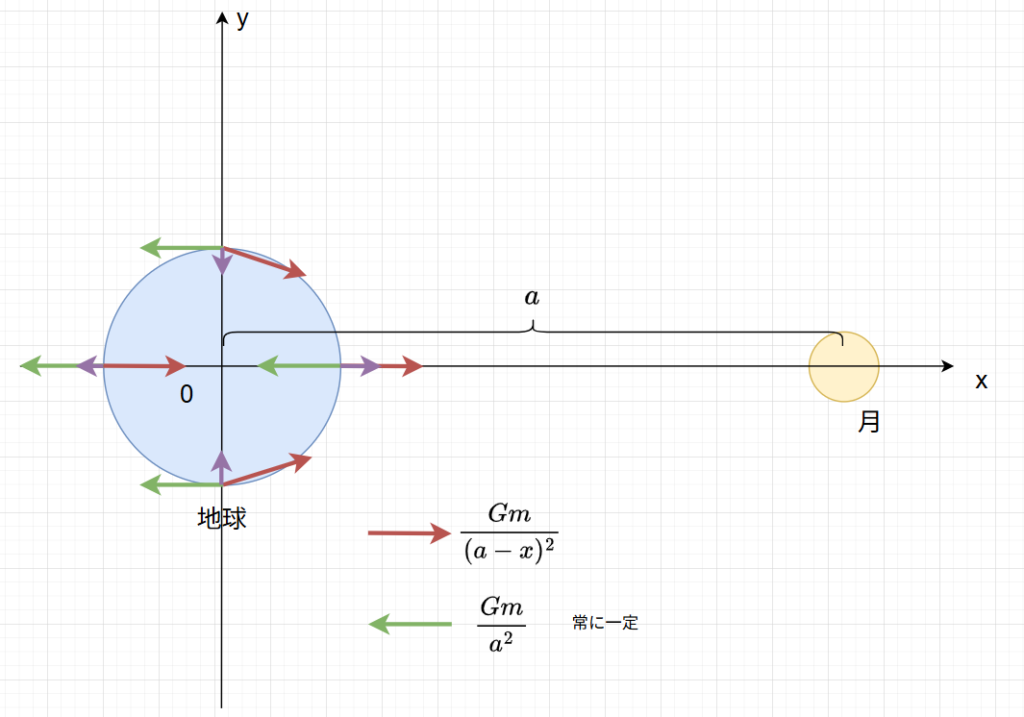
よって、ラグビー型になる訳です。

潮汐力をもとめてみる
ここからは潮汐力の式を求めてみます。
2つのアプローチで求めてみます。
- $x$軸上の点から求める
- ポテンシャルエネルギーから求める
です。
$x$軸上の点から潮汐力を求める
$x << a$のとき(地球の半径が月までの距離よりずっと小さい時)を考えます。
上記にも記載の通り、地球上のある点が月から受ける重力加速度は$ \frac{G m}{(a-x)^2} $でした。
ここでは$G$と$m$は定数なので一旦置いておいて、その2つを除いた$\frac{1}{(a-x)^2}$を考えます。
関数$\frac{1}{(a-x)^2}$をテイラー展開すると
$$\frac{1}{(a-x)^2} = \frac{1}{a^2}+\frac{2x}{a^3}+\frac{3x^2}{a^4}+…. $$
となります。
地球の半径は6,356km、地球と月との距離は380,000km、月の半径は1,738kmとすると、$x=6356$、$a=388094$となり、
第2項の$\frac{2x}{a^3}$は$\frac{2×6356}{388094^3}$となりかなり小さい数字になる事が分かります。
よって、$a^4$となる3項目はさらに小さくなり、4項目以降はそれよりもさらに小さい数字になります。
よって、第3項目以降は無視できるものとし、以下の近似式が出てきます。
$$\frac{1}{(a-x)^2} \approx \frac{1}{a^2}+\frac{2x}{a^3}$$
このため、$ f=\frac{G m}{(a-x)^2} $は以下の近似式で表すことができます。
$$ f=\frac{G m}{(a-x)^2} \approx \frac{G m}{a^2}+\frac{2 G m}{a^3} x $$
少し注意点として、万有引力の式が$\frac{G m M}{r^2}$なので、月から受ける力で紛らわしいですが、ここでは「地球が月から受ける力」ではなく、「地球上の点(単位質量の点)が月から受ける重力加速度」を扱っています。
1項目($\frac{G m}{a^2}$)は 地球全体が月から受ける一様な重力(もしくは地球中心での月の重力)を表しています。
2項目($\frac{2 G m}{a^3} x$)は「地上の点」と「地球中心」の月の重力の差で、これが潮汐力となります。
月に近い側では月の重力が慣性力よりも大きくなることで、潮汐力が大きくなりますし、一方で、月と反対側では慣性力が月の重力よりも大きくなるので、月とは反対向きの力が大きくなるという事です。
ここで、潮汐力が地球の公転運動と関係なく出てきています。
これは公転運動と潮汐力とは関係ないという事を表しており、公転運動による遠心力は考慮しないで求めることができるという事です。
ポテンシャルエネルギーから潮汐力を求める
力を扱う時はベクトル式が出てきて、座標方向を考慮する必要がでてきます。
ポテンシャルは位置エネルギーなので、スカラーとなり向きは考えずに良くなります。
また、ポテンシャルの式を座標方向に微分して符号を変えることで力の式が得られます。
なので、ここでのアプローチはポテンシャルを求めてから$x$と$y$で微分することで求めます。
—
地球と月が存在する空間において、ある点 $(x, y, z)$ に質量 1の「試験質量」を置いたときの
重力ポテンシャル $V$ の合計は以下の式で表されます。
$$ V=-\frac{G M}{\sqrt{x^2+y^2+z^2}}-\frac{G m}{\sqrt{(x-a)^2+y^2+z^2}} $$
- 地球の質量 $M$
- 月の質量 $m$
です。
これはすなわち、以下を示しています。
$$ V = V_{\text{地球}} + V_{\text{月}} = -\frac{GM}{r_{\text{地球}}} – \frac{Gm}{r_{\text{月}}} $$
さて、ここでポテンシャルが何故マイナスなのでしょうか。
💡ポテンシャルがマイナスになる理由
ポテンシャルは位置エネルギーです。
ここでは重力によるポテンシャルエネルギーを表したい。
重力は距離がどんなに離れていても働き続けます。(無限に減衰していくんだけど、完全には消えません)
そんな重力がもうこれ以上働かない場所を無限遠方に設定します。
これが基準になります。
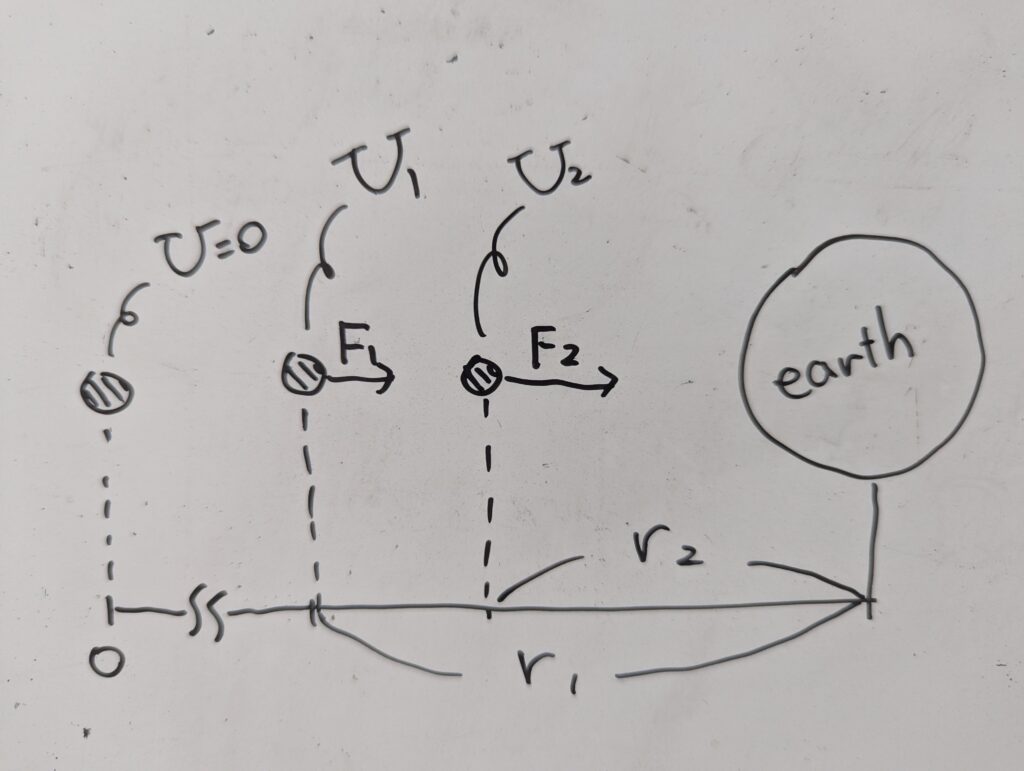
以下のような状況です。一番左が基準でこの時のポテンシャルエネルギー$U$は$0$です。
さて、ここで、一般的な位置エネルギーについて考えます。
以下のような場合、

- 左の場合:基準を地面にしているため位置エネルギーは$mgh$($m$は質量、$g$は重力、$h$は高さ)
- 右の場合:基準を崖の上にしているため、位置エネルギーは$-mgh$
左の場合はエネルギーがあるのでそのままだと落下します。エネルギーが運動に変わる訳です。
一方で、右側は持ち上げるという外部の力が無いと基準まで到達できません。
よって、エネルギーはマイナス(外部から力を加えることで、基準まで持ち上げ、その時点で$U=0$)となります。
さて、では、先ほどの画像に戻りましょう。

無限遠方を基準に置いており、引力によって引っ張られている対象からすると、まず、$U_1$に関しては、元の基準に戻ろうとするには別の外部から力をかける必要があります。
つまり、先ほどの崖の下に物体がある時の位置エネルギーと同じ考え方ができます。
だからマイナスなのです。
ちなみに、${r_1} > {r_2}$なので、
$\frac{G M}{{r_1}^2} < \frac{G M}{{r_2}^2}$
となります。
これは距離が基準から遠いほど、元に戻す力がより必要だという事を表しています。
さて、
$$ V=-\frac{G M}{\sqrt{x^2+y^2+z^2}}-\frac{G m}{\sqrt{(x-a)^2+y^2+z^2}} $$
に戻りましょう。
この式の第1項は地球の重力ポテンシャルで、第2項が月の重力ポテンシャルなので、
この式の第2項 $-\frac{G m}{\sqrt{(x-a)^2+y^2+z^2}}$に着目します。(これを$V_m$とおきます。)
$$ -\frac{G m}{\sqrt{(x-a)^2+y^2+z^2}} = -\frac{G m}{\sqrt{a^2-2ax+x^2+y^2+z^2}} = -\frac{G m}{a\sqrt{1-\frac{2x}{a}+\frac{x^2+y^2+z^2}{a^2}}} $$
となります。
📜📜📜
そして、$GM$をとった$\frac{1}{a\sqrt{1-\frac{2x}{a}+\frac{x^2+y^2+z^2}{a^2}}}$の部分を考えます。※1
$x^2+y^2+z^2$は地球の中心からある点までの距離$r$の2乗になるので、$x^2+y^2+z^2=r^2$であり
$$ \varepsilon = -\frac{2x}{a}+\frac{r^2}{a^2} $$とすると、
$\varepsilon$のテイラー展開で、以下の様になります。
$$ (1 + \varepsilon)^{-1/2} = 1 – \frac{1}{2} \varepsilon + \frac{3}{8}\varepsilon^2 – \cdots $$
ここで$\varepsilon = -\frac{2x}{a}+\frac{r^2}{a^2}$を元に戻します。
$$ \begin{eqnarray} \frac{1}{a\sqrt{1-\frac{2x}{a}+\frac{x^2+y^2+z^2}{a^2}}} = \frac{1}{a}{1 – \frac{1}{2}(\frac{2x}{a}+\frac{r^2}{a^2}) + \frac{3}{8}{(\frac{2x}{a}+\frac{r^2}{a^2})}^2 – \cdots} \\\\ = \frac{1}{a}{1 + \frac{x}{a} + \frac{3x^2-2r^2}{2a^2} + \cdots}\end{eqnarray}\ $$
となります。
この時、$x$は$a$と比べて十分に小さく、
上記式の$\frac{3x^2-2r^2}{2a^2}$以降は無視できるものとします。
上記※1のところで$Gm$を外したので、最後に$Gm$を付けてあげると、
$$-\frac{G m}{\sqrt{(x-a)^2+y^2+z^2}} \approx \frac{1}{a} + \frac{x}{a^2} + \frac{3x^2-2r^2}{2a^3}$$
が求まります。
$r^2=x^2+y^2+z^2$を代入して整理すると、
$$ -\frac{G m}{a}-\frac{G m}{a^2}x-\frac{G m}{a^3}(x^2-\frac{1}{2}y^2-\frac{1}{2}z^2) $$
が求まります。
力(加速度)はポテンシャルの勾配(傾き)から決まり、
$$ \vec{a}=-\nabla V=-\left(\frac{\partial V}{\partial x}, \frac{\partial V}{\partial y}, \frac{\partial V}{\partial z}\right) $$
となります。
傾きなので微分するってことで、これは定数は消えてしまいます。
つまり、$-\frac{G m}{a}$は定数なので無視することになります。
第2項目の$-\frac{G m}{a^2}x$は加速度系で見た時の地球の重力のポテンシャルです。
よって、残りの第3項である、$-\frac{G m}{a^3}(x^2+\frac{1}{2}y^2+\frac{1}{2}z^2)$が潮汐力に該当します。
上記でも書いたように、力(加速度)はポテンシャルの勾配(傾き)から求めることができるので、
$x$軸方向の潮汐力の加速度は
$$-\frac{\partial }{\partial x}(-\frac{G m}{a^3}(x^2-\frac{1}{2}y^2-\frac{1}{2}z^2)) = \frac{2Gm}{a^3}x$$
となり、
$y$軸方向の潮汐力の加速度は
$$-\frac{\partial }{\partial y}(-\frac{G m}{a^3}(x^2-\frac{1}{2}y^2-\frac{1}{2}z^2)) = -\frac{Gm}{a^3}x$$
となります。
最後に
難しかったけど、潮汐力を求めることができて、満ち潮引き潮がラグビー型になる理由も納得することができました。