M-1の決勝でハロー効果が発生しているのか調べる

はじめに
調べ方について（カイ二乗検定）
1. カイ二乗検定（Chi-Square Test）とは
2. 各値について
pythonでもとめる
1. pythonコード
2. 結果

はじめに

去年の年末も、熱いM-1が開催されました。

令和ロマン、優勝おめでとうございます！

2年連続の快挙は本当にすごいですね。

さて、M-1の決勝の方式は1回戦と2回戦に分けられて実施されます。

1回戦めで10組のコンビが漫才を行い、その漫才に審査員が点数を付けます。

点数の上位3組が2回戦へと進出。

2回戦目に進出したコンビの中から審査員によって優勝者が決定されます。

さて、ここで僕は一つの疑問を抱きました。

1回戦めの点数によって2回戦目の漫才の評価に影響があるのではないかと。

というのも、ハロー効果というものがあり、人がある対象（人、物、ブランドなど）の一つの目立った特徴を見て、それに引きずられて他の特徴も同じように評価してしまう心理現象です。

例えば、成績が良い生徒は「行動もきちんとしている」と教師に思われたりです。

一次試験の結果が良いと、試験官や面接官はその受験者に対して「頭が良い」「優秀そう」というポジティブな印象を持ちやすくなり、この印象が、二次試験（例えば面接や実技）の評価に影響を与えることがあります。

もし、それがあるとするのであれば、M1でも1回戦目の影響が2回戦に影響してしまうことが言えます。

そこで、1回戦目の評価が2回戦目に影響がないかどうかを調べてみました。

調べ方について（カイ二乗検定）

調べる方法はカイ二乗検定を用います。

手順としては、クロス集計表を作成し、その後、カイ二乗検定を実施します。

結果をp値に基づいてハロー効果が優勝者決定の際の判定に影響してしまっているのかを判断します。

カイ二乗検定を実施といっても、具体的な実施内容を記載しないと分からないと思うので、実際に調べる前に、カイ二乗検定についても記載しておきます。（興味が無ければ結果まで飛ばしてくださいw）

カイ二乗検定（Chi-Square Test）とは

カイ二乗検定とはは、「2つのデータが関連しているかどうか」を調べるための統計的な方法で、2つの変数が独立しているかどうかを検定するのに使われます。

「観測データ（実際のデータ）と期待されるデータ（仮説に基づくデータ）との間にズレがあるかどうか」を確認し、このズレが大きければ「関係があるかも！」、小さければ「特に関係なさそう」と判断します。

カイ二乗検定の手順は以下のような流れです。

仮説を立てる
- 帰無仮説（H0）: 2つの変数には関係がない
- 対立仮説（H1）: 2つの変数には関係がある
期待される頻度を計算
帰無仮説（関係がないと仮定）に基づいて、各カテゴリにどれだけの数が期待されるか（期待頻度）を計算
カイ二乗値を計算
観測データと期待データのズレを数値化し、カイ二乗値を計算します。この値が大きいほど、観測データが期待データから大きくズレていることを意味します。
p値を使って判断
p値を確認し、統計的に意味のあるズレかどうかを判断します。通常、p値が0.05未満の場合は「関係がある」と判断し、帰無仮説を棄却します。

各値について

カイ二乗値（Chi-Square Statistic）
- 観測されたデータと期待されるデータの間の差を表す
- 具体的には、実際に観測された頻度と、もし帰無仮説が正しいとした場合に期待される頻度とのズレを表す
p値
- 帰無仮説が正しいと仮定した場合に、観測されたデータが得られる確率
  - p値が小さい（一般的には0.05未満）場合、観測されたデータは帰無仮説が正しいとするには非常に珍しいため、帰無仮説を棄却する
  - p値が大きい場合、観測されたデータは帰無仮説が正しいことを示唆するため、帰無仮説を採択する
自由度
- 検定において独立して変動できるデータの数を表す
- 自由度は、検定の分布を決定するために必要で、自由度が増えると、カイ二乗分布がより正規分布に近づく
期待頻度
- 帰無仮説が正しいと仮定した場合に、各カテゴリで期待される観測数

pythonでもとめる

上記で示したカイ二乗検定をpythonで書いて、ハロー効果の影響をM1の審査基準に影響してしまっているかを調べてみます。

pythonコード

pythonコードは以下のようになっています。

import pandas as pd
import numpy as np
from scipy.stats import chi2_contingency
import statsmodels.api as sm
import statsmodels.formula.api as smf

df = pd.read_excel("m1_data.xlsx")
df['Score'] = df['Score'].astype(str).str.extract('(\d+)').astype(int)
df['Rank'] = df.groupby('Year')['Score'].rank(method='min', ascending=False)

# 得点順位と面接結果のクロス集計表を作成
contingency_table = pd.crosstab(df['Rank'], df['Selected'])

# カイ二乗検定を実施
chi2, p, dof, expected = chi2_contingency(contingency_table)

# 結果を表示
print("\nクロス集計表:")
print(contingency_table)
print(f"\nカイ二乗値: {chi2}")
print(f"p値: {p}")
print(f"自由度: {dof}")
print("期待頻度:\n", expected)

# 結果の解釈
alpha = 0.05
if p < alpha:
    print("決勝一回戦めの得点順位が2回戦目に影響を与えている（帰無仮説を棄却）")
else:
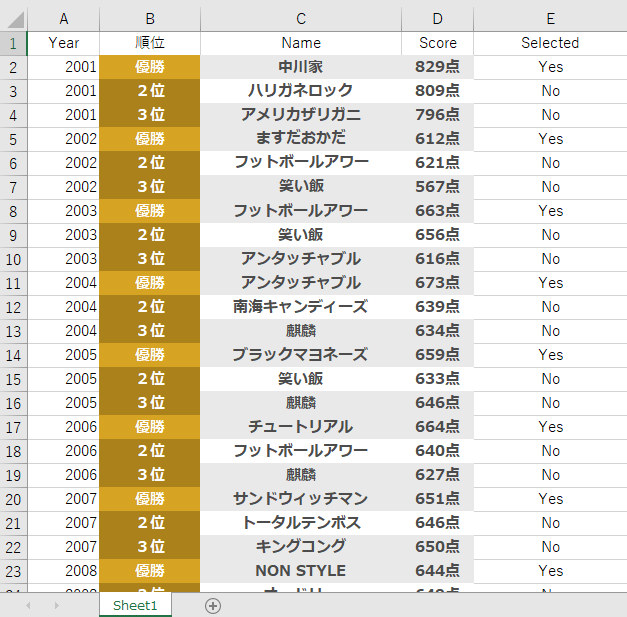
    print("決勝一回戦めの得点順位は2回戦目に影響を与えていない（帰無仮説を採択）")

m1_data.xlsxは以下のようなデータとなっています。

結果

気になる結果は…

クロス集計表:
Selected  No  Yes
Rank
1.0       11   10
2.0       13    7
3.0       16    3

カイ二乗値: 4.58515037593985
p値: 0.1010060171704983
自由度: 2
期待頻度:
 [[14.          7.        ]
 [13.33333333  6.66666667]
 [12.66666667  6.33333333]]
決勝一回戦めの得点順位は2回戦目に影響を与えていない（帰無仮説を採択）

となりました。

「決勝一回戦めの得点順位は2回戦目に影響を与えていない」

となり、ハロー効果見られませんでした。