あらすじ
前回までの精度改善では、大幅な精度改善と分析までができました。😄
今回すること
今回は遺伝的アルゴリズムを試してみたいと思います。
以前、コスパ指数ということで以下の式を求めました。
$$ CP = T_{s} – T_{v} $$ (ジャンルごとの評価値の偏差値を$T_{s}$、ジャンルごとの価格帯の偏差値を$T_{v}$とする)
要は評価値が高くなり、価格帯が低いという指標を設けました。
ぶっちゃけ、これだけだと、あまり良い指標ではなかったと思います。
で、ここでの問いは、評価値を最大にして、価格帯を最小にするという、2つの変数の最適化を実施しようと思います。
今回は、遺伝的アルゴリズムを用いて2変数の最適解を求めます。
食べログの評価値の最適解と価格帯の最適解(できるだけ評価値が高くて、できるだけ価格帯が低い値)を求めるのです。
しかし、如何せん僕が遺伝的アルゴリズムを使ったこともなく、まずはどんなものかのデモをしてみたかったので前段としてこの記事にしました。
素人ながら、ネットの記事やChatGPTを駆使して何とかプログラムコードを書きましたので、間違いがあるかもしれません。
もしありましたら、ご指摘よろしくお願いいたします!!
今回の例題(デモ)
今回は駄菓子屋さんを例にとって考えます。

駄菓子1つに対して値段とその駄菓子を購入したときに得られる嬉しさ度の2変数を設けます。
例えばうまい棒のコーンポタージュ味なら10円で嬉しさ度40に対して、うまい棒のサラダ味は10円に対して嬉しさ度30とします。
この時、うまい棒コーンポタージュ味は[値段, 嬉しさ度] = [10, 40]という2変数で表されますし、うまい棒サラダ味は[値段, 嬉しさ度] = [10, 30]で表されます。
今回は一番高い駄菓子でも1000円までの商品しか扱っていない駄菓子屋という設定で行います。
ちなみに一番高い駄菓子に関しては「えがちゃんねる」様が投稿した以下動画にて大人買いのスルメが2280円で一番高かったです。
なので、駄菓子の価格の取り得る値の最大値を2280とします。
で、これが食べログの結果にどうつなげていくかというと、値段が価格帯に相当し、満たされる嬉しさ度が評価値に相当します。
今回はこの駄菓子屋の設定で検証デモを行います。
実践
そもそも、遺伝的アルゴリズムとは

遺伝的アルゴリズムは自然淘汰の仕組みを応用した最適化問題を解くための手法です。
以下が遺伝的アルゴリズムの手順です。
①初期集団の生成:
- 個体を表す染色体をランダムに生成
- 各染色体はパラメータの組み合わせを表す
②適応度の評価:
- 各個体の適応度を評価する
- 評価は目的関数に基づいて評価する
- 今回の目的関数は評価値を最大化し、価格帯を最小化する
③選択:
- 適応度に基づいて、個体を次の世代に選択する
- 適応度が高い個体ほど選ばれやすくなる
④交叉:
- 選択された個体をもとに、交叉操作を行い子孫を生成する
- 交叉は染色体の一部を交換することで新たな個体を生成する
⑤突然変異:
- 生成された子孫の一部の遺伝子を突然変異させる
- 突然変異はランダムな変更を加えることで探索空間を広げる
pythonコード
では、上記の遺伝的アルゴリズムをpythonに落とし込むとどうなるのでしょうか。
今回の全体の実装コードは以下になります。
import random
import numpy as np
from sklearn.neural_network import MLPRegressor
from deap import base, creator, tools, algorithms
import numpy as np
import matplotlib.pyplot as plt
# 突然変異操作をカスタマイズ
def custom_mutation(individual):
a_min = 1
a_max = 50
b_min = 10
b_max = 2280
# 突然変異の強度(範囲)を設定
mutation_strength = 5 # 例: 突然変異が変数に与える影響の大きさ
# aの突然変異
individual[0] += random.uniform(-mutation_strength, mutation_strength)
# 範囲外の値を制約内に収める
individual[0] = max(a_min, min(a_max, individual[0]))
# bの突然変異
individual[1] += random.uniform(-mutation_strength, mutation_strength)
# 範囲外の値を制約内に収める
individual[1] = max(b_min, min(b_max, individual[1]))
def objective_function(individual):
a, b = individual
#正規化
a = (a - 1)/(50 - 1)
b = (b - 10)/(2280 - 10)
# 目的関数の定義例:a を最大化し、b を最小化する
return a - b
# 最適化問題の設定
## 適応度クラスの作成
creator.create("FitnessMulti", base.Fitness, weights=(1.0, -1.0)) # a を最大化、b を最小化
## 個体クラスの作成 listクラスを継承し、適応度クラスのcreator.FitnessMinを属性として持つ
creator.create("Individual", list, fitness=creator.FitnessMulti)
## Toolboxには様々な関数を指定した名前で登録することができる
toolbox = base.Toolbox()
## 遺伝子を生成する関数"attr_gene"を登録
## 初期個体の遺伝子を0から10の間でランダム(random.uniform)に作成
toolbox.register("attr_float", random.uniform, 0, 1000)
## 個体を生成する関数”individual"を登録
## tools.initRepeatの引数としてcreator.Individual, toolbox.attr_gene, 2を登録
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_float, n=2)
## 個体集団を生成する関数"population"を登録
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
## 評価関数"evaluate"を登録
toolbox.register("evaluate", objective_function)
## 交叉を行う関数"mate"を登録
toolbox.register("mate", tools.cxBlend, alpha=0.2)
## 変異を行う関数"mutate"を登録
toolbox.register("mutate", custom_mutation)
## # 個体選択法"select"を登録
toolbox.register("select", tools.selTournament, tournsize=3)
def main():
cost_list = []
list_1 = list(range(10, 101, 10))
list_2 = list(range(120, 301, 10))
list_3 = list(range(350, 1001, 50))
cost_list = list_1 + list_2 + list_3
item_cost_values = []
value_probabilities = [
1.0, 0.90, 0.90, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85,
0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.83, 0.83,
0.83, 0.81, 0.80, 0.78, 0.75, 0.75, 0.75, 0.75,
0.75, 0.5, 0.5, 0.5, 0.4, 0.3, 0.2, 0.2, 0.2, 0.2,
0.2, 0.2, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1
]
# 10000個のランダムな値を生成
for _ in range(10000):
# 値をランダムに選ぶ
selected_value = random.choices(cost_list, weights=value_probabilities)[0]
item_cost_values.append(selected_value)
ureshii_values = []
for i in item_cost_values:
if i <= 80:
ureshii_values.append(random.randint(5, 30))
elif 80 < i and i <= 200:
ureshii_values.append(random.randint(10, 35))
elif 200 < i and i <= 500:
ureshii_values.append(random.randint(15, 40))
else:
ureshii_values.append(random.randint(20, 45))
custom_individuals = list(zip(ureshii_values, item_cost_values))
population = [creator.Individual(ind) for ind in custom_individuals]
#print("population:", population)
CXPB, MUTPB, NGEN = 0.5, 0.05, 1001 # 交叉率、突然変異率、世代数
#print("Start of evolution")
# Evaluate the entire population
fitnesses = [objective_function(individual) for individual in population]
print(" Evaluated %i individuals" % len(population))
## 進化ループ開始
for gen in range(NGEN):
if (gen % 50 == 0):
print("-- Generation %i --" % gen)
# 次世代個体の選択・複製
offspring = toolbox.select(population, len(population))
offspring = list(offspring)
## 交叉
for child1, child2 in zip(offspring[::2], offspring[1::2]):
# 交叉させる個体を選択
## 次世代個体候補から個体を2個ずつ選択肢、確率CX_PBで個体同士の交叉を実施
if random.random() < CXPB:
toolbox.mate(child1, child2)
## 交叉を実行した個体のfitness属性は後で再設定するために一旦削除
del child1.fitness.values
del child2.fitness.values
## 変異
for mutant in offspring:
## 変異させる個体を選択
if random.random() < MUTPB:
toolbox.mutate(mutant)
# 変異させた個体は適応度を削除する
del mutant.fitness.values
## 適応度を削除した個体について適応度の再評価を行う
## 交叉あるいは変異を行った個体は遺伝子が変化しているので、適応度(fitness属性)を再評価する必要がある
#fitnesses = [objective_function(a_gene, b_gene) for a_gene, b_gene in population]
fitnesses = [objective_function(individual) for individual in population]
if (gen % 50 == 0):
print(" Evaluated %i individuals" % len(offspring))
# 個体集団を新世代個体集団で更新
population[:] = offspring
print("-- End of (successful) evolution --")
best_ind = tools.selBest(population, 1)[0]
print("Best individual is %s" % (best_ind))
if __name__ == "__main__":
main()以下で部分的にコードを説明します。
初期個体の生成
まず、最初の個体を生成する必要があります。
個体を生成しているところは以下の部分になります。
cost_list = []
list_1 = list(range(10, 101, 10))
list_2 = list(range(120, 301, 10))
list_3 = list(range(350, 1001, 50))
cost_list = list_1 + list_2 + list_3
item_cost_values = []
value_probabilities = [
1.0, 0.90, 0.90, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85,
0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.83, 0.83,
0.83, 0.81, 0.80, 0.78, 0.75, 0.75, 0.75, 0.75,
0.75, 0.5, 0.5, 0.5, 0.4, 0.3, 0.2, 0.2, 0.2, 0.2,
0.2, 0.2, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1
]
# 1000個のランダムな値を生成
for _ in range(10000):
# 値をランダムに選ぶ
selected_value = random.choices(cost_list, weights=value_probabilities)[0]
item_cost_values.append(selected_value)
ureshii_values = []
for i in item_cost_values:
if i <= 80:
ureshii_values.append(random.randint(5, 30))
elif 80 < i and i <= 200:
ureshii_values.append(random.randint(10, 35))
elif 200 < i and i <= 500:
ureshii_values.append(random.randint(15, 40))
else:
ureshii_values.append(random.randint(20, 45))
custom_individuals = list(zip(ureshii_values, item_cost_values))
population = [creator.Individual(ind) for ind in custom_individuals]駄菓子は金額が少ない方の商品は色々あるだろうけど、金額が高い商品は少ないと思ったので、金額が高い商品は少なめに設定しました。
ヒストグラムにすると以下のような感じ。
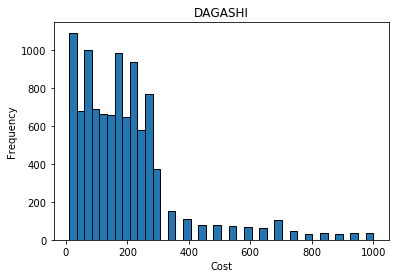
で全体として金額が高い商品の方が買った時の嬉しさ度が高くなりそうだなと思ったので、そこも調整しています。
ヒストグラムのヒートマップにすると以下のような感じ。
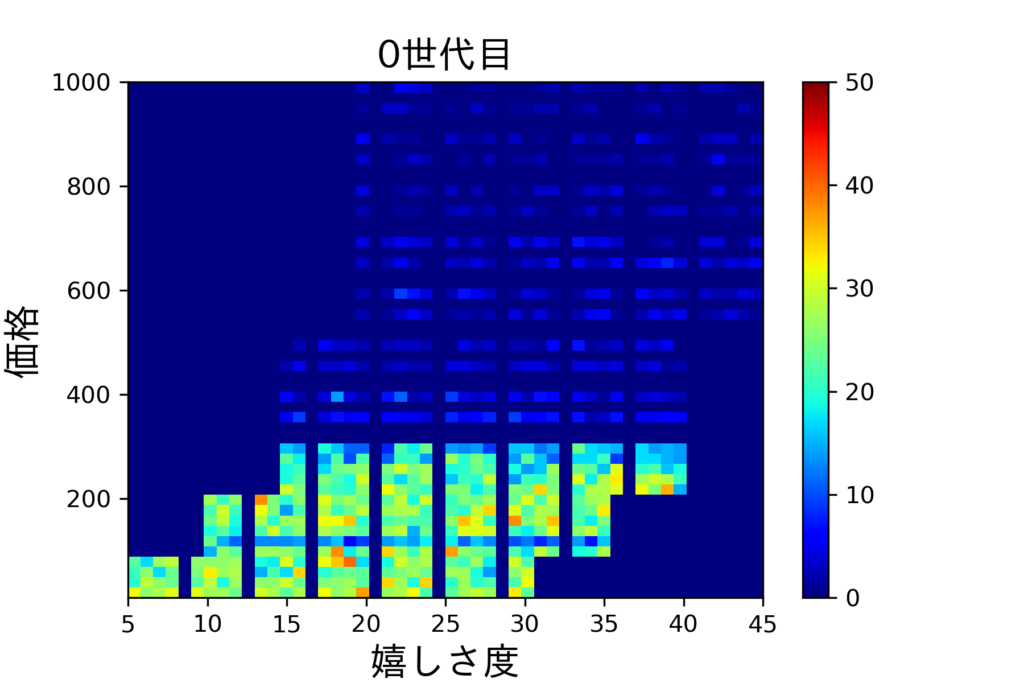
目的関数
目的関数は今回だと、価格を下げて、嬉しさ度を上げるような関数を用意しないといけません。
ということで、以下のようなコードとしました。
def objective_function(individual):
a, b = individual
#正規化
a = (a - 1)/(50 - 1)
b = (b - 10)/(2280 - 10)
# 目的関数の定義例:a を最大化し、b を最小化する
return a - baが嬉しさ度で、bが価格とします。
ハイライトの部分は正規化を行っています。
これは、嬉しさ度と価格が単純に引き算で求めると、レンジ(10~2280円)の大きい価格の値の影響の方が大きくなってしまうことを懸念したためです。
突然変異
突然変異は自分で関数を用意しました。
発生する個体の嬉しさ度と価格は値の範囲に決まりがあるからです。
コードとしては以下のような感じ。
def custom_mutation(individual):
a_min = 1
a_max = 50
b_min = 10
b_max = 2280
# 突然変異の強度(範囲)を設定
mutation_strength = 5 # 例: 突然変異が変数に与える影響の大きさ
# aの突然変異
individual[0] += random.uniform(-mutation_strength, mutation_strength)
# 範囲外の値を制約内に収める
individual[0] = max(a_min, min(a_max, individual[0]))
# bの突然変異
individual[1] += random.uniform(-mutation_strength, mutation_strength)
# 範囲外の値を制約内に収める
individual[1] = max(b_min, min(b_max, individual[1]))結果
結果の出力は以下のようになりました。
Best individual is [35.392861131446324, 249.69564240458698]
ということで、嬉しさ度は35ぐらいで250円の駄菓子が遺伝的アルゴリズムだと最適な答えとなるとのことです。
また、ヒートマップの推移は以下になります。(世代ごとにヒートマップ横のバー最大値を変えていますのでご注意ください)
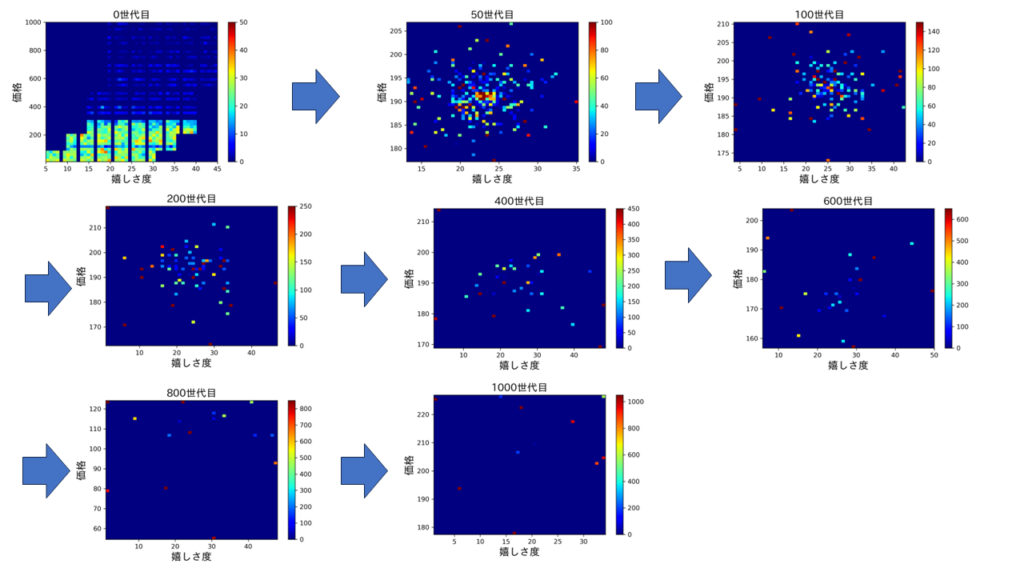
ある一点に収束するというより、幾つかのの点に収束しました。
まとめ
今回はシミュレーションとして駄菓子屋の例で遺伝的アルゴリズムを実装してみました。
遺伝的アルゴリズムを理解し、それをコードとして実装するということができ、一歩成長できました。
次回は実際に食べログ(北海道)のデータを用いて試してみます。
というか、駄菓子が食べたくなってきましたね。
よかったらおひとついかがですか??
その他、お菓子の広告


