はじめに
前回はLSTMを使って気温を学習してみました。
今回はその学習したモデルを使用して、予測ができるかを確認します。
今回も前回に引き続き、参考にするサイトは以下です。

とても素晴らしい記事です。
予測の実装
モデルの評価(予測)
テストデータを正規化してTensor型に変換します。
予測するためのデータの最初のseq_length分はtrain_dataの最後の部分を使用します。
# 予測する時間
pred_h = 1757
# テストデータの正規化
test_data_normalized = scaler.fit_transform(test_data)
#Tensor型に変換
test_data_normalized = torch.FloatTensor(test_data_normalized)
# 予測するためのデータの最初のseq_length分はtrain_dataを使用
test_inputs = train_data_normalized[-seq_length:].tolist()モデルを評価します。
model.eval()
test_outputs = []
for i in range(pred_h):
seq = torch.FloatTensor(test_inputs[-seq_length:])
seq = torch.unsqueeze(seq, 0)
seq = seq.to(device)
with torch.no_grad():
test_inputs.append(test_data_normalized.tolist()[i])
test_outputs.append(model(seq).item())グラフで表示させるために予測結果のリストをNumPy配列に変換します。
np_test_outputs = np.array(test_outputs).reshape(-1,1)
np_test_outputs2 = np.hstack((np_test_outputs, np_test_outputs))
np_test_outputs3 = np.hstack((np_test_outputs2, np_test_outputs))
actual_predictions = scaler.inverse_transform(np_test_outputs3)こちらのコードに関しては、予測結果のリストをNumPy配列に変換しているしています。
具体的には、
np_test_outputs = np.array(test_outputs).reshape(-1,1)に関しては、test_outputsは1次元の[y1, y2, …, yN]のリストです。
.reshape(-1, 1)の部分は配列を 2次元に変換し、行数は自動(-1)で決定されています。
よって、
[y1, y2, ..., yN] → [[y1], [y2], ..., [yN]]となります。
次に、
np_test_outputs2 = np.hstack((np_test_outputs, np_test_outputs))ですが、np_test_outputs を水平方向に結合し、2列の配列を作成します。
np.hstackは配列を水平方向(列方向)に結合します。
結果として、以下のようになります。
[[y1, y1],
[y2, y2],
...,
[yN, yN]]次の
np_test_outputs3 = np.hstack((np_test_outputs2, np_test_outputs))も同じ要領で、np_test_outputs3は
[[y1, y1, y1],
[y2, y2, y2],
...,
[yN, yN, yN]]となります。
この3行N列の配列をもとのスケールに戻すために次のコードがあります。
actual_predictions = scaler.inverse_transform(np_test_outputs3)で、以下のような結果になります。
[[original_y1, original_y1, original_y1],
[original_y2, original_y2, original_y2],
...,
[original_yN, original_yN, original_yN]]グラフを表示します。
実際の気温に、予測した気温のグラフを重ねて表示ます。
fig_size = plt.rcParams['figure.figsize']
fig_size[0] = 10
fig_size[1] = 5
plt.rcParams['figure.figsize'] = fig_size
plt.title('temperature')
plt.ylabel('temperature')
plt.grid(True)
plt.autoscale(axis='x', tight=True)
plt.plot(feature_data['気温(℃)'], label='temperature')
plt.plot(x, actual_predictions[:,0], label='prediction')
plt.xlabel('date')
plt.legend()
plt.show()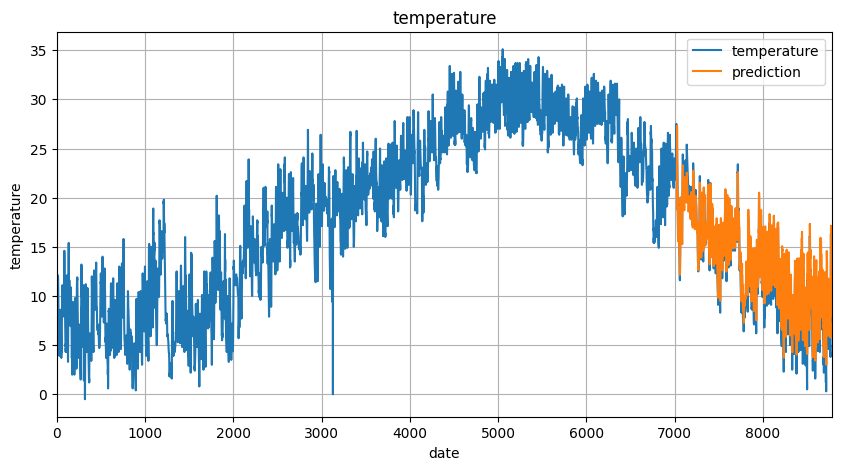
より見やすくするために、実際のグラフと予測したグラフが重なっているところだけを表示します。
plt.title('temperature')
plt.ylabel('temperature')
plt.grid(True)
plt.autoscale(axis='x', tight=True)
plt.plot(x, feature_data['気温(℃)'][-1*pred_days:], label='temperature')
plt.plot(x, actual_predictions[:,0], label='prediction')
plt.xlabel('date')
plt.legend()
plt.show()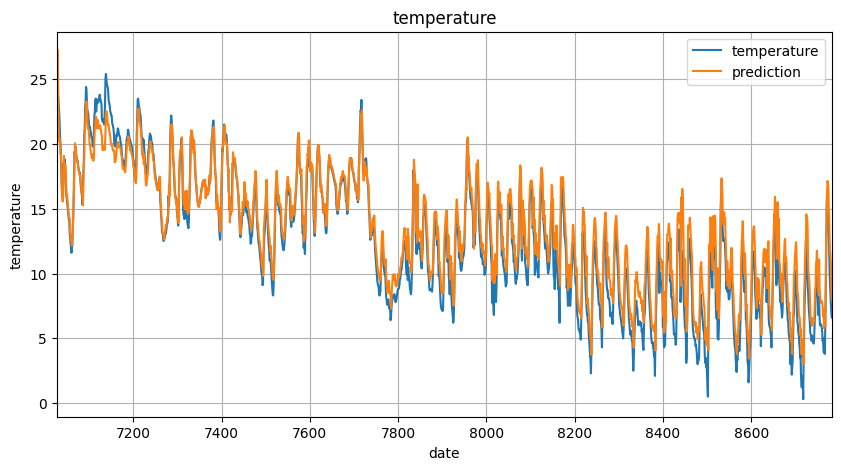
なんか、怖いぐらい精度がいいですね。。。
さらにその先を予測
上記の評価よりさらに先を予測してみます。
今回使用したデータは2024年の12/31までなので、2025年以降を予測させてみて、実際の値と比較させてみます。
上記ではtrain_dataを使用しましたが、今回は今回使用したデータのさらに先を予測するので、今回のデータの最後のデータであるtest_dataを使用します。
test_data_normalized = scaler.fit_transform(test_data)
test_data_normalized = torch.FloatTensor(test_data_normalized)
# 予測するためのデータの最初のseq_length分はtest_dataを使用
test_inputs = test_data_normalized[-seq_length:].tolist()モデルを評価します。
今回のデータより120時間先の値までを予測します。
pred_h = 120
model.eval()
# 予測値を入れるリスト
test_outputs = []
for i in range(pred_h):
seq = torch.FloatTensor(test_inputs[-seq_length:])
seq = torch.unsqueeze(seq, 0)
seq = seq.to(device)
with torch.no_grad():
# 元データが残っている場合はそれを使用、なければモデルの予測値を使う
if i < seq_length:
next_input = test_data_normalized.tolist()[-1*seq_length + i] # 元データ
else:
next_input = [test_outputs[-1], 0.0, 0.0] # モデルの予測値を使用
# 次の入力をtest_inputsに追加
test_inputs.append(next_input)
# モデルで予測を行い、結果を保存
test_outputs.append(model(seq).item())グラフで表示させるために予測結果のリストをNumPy配列に変換します。
np_test_outputs = np.array(test_outputs).reshape(-1,1)
np_test_outputs2 = np.hstack((np_test_outputs, np_test_outputs))
np_test_outputs3 = np.hstack((np_test_outputs2, np_test_outputs))
actual_predictions = scaler.inverse_transform(np_test_outputs3)グラフで表示します。(※ xlabelをdateにしてしまいましたが、hourの間違えです。。。)
fig_size = plt.rcParams['figure.figsize']
fig_size[0] = 20
fig_size[1] = 5
plt.rcParams['figure.figsize'] = fig_size
plt.title('temperature')
plt.ylabel('temperature')
plt.grid(True)
plt.autoscale(axis='x', tight=True)
plt.plot(actual_predictions[:,0], label='prediction')
plt.xlabel('date')
plt.legend()
plt.show()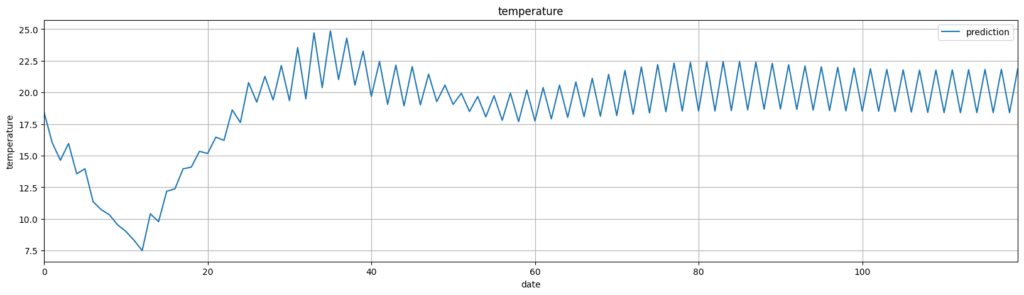
30時間あたりから怪しくなって、70時間後あたりから完全に周期的な値を摂るようになってしまっています。
では、シークエンスを120hに増やしてみます。(10日分です)
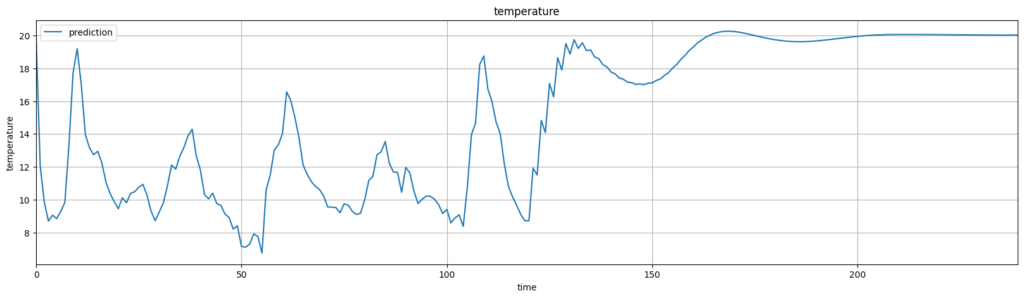
なるほど、120時間まではかろうじて予測がまともにできています。
シーケンス長が長い方がより未来を予測できそうです。
では、実際の気温と比較してみます。
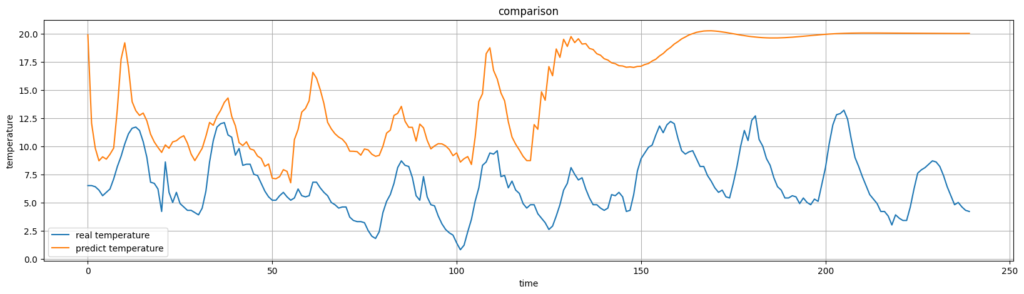
120hあたりまで動きは似ていますね。
しかし、値は、50hぐらいまでしか近い値を維持できていませんね。
最後に
もっと多くの値を使用すれば、より正確で、より長い期間の予測ができるかもしれませんね。


