はじめに
「風が吹けば桶屋が儲かる」という言葉を聞いたことがあるでしょうか。
これは、一見関係なさそうな出来事が連鎖して、意外な結果につながることを表すことわざです。
例えば、風が吹く → 砂ぼこりが舞う → 盲人が増える → 三味線を弾く人が増える → 三味線に使う猫の皮が必要になる → 猫が減る → ネズミが増える → ネズミが桶をかじる → 桶屋の需要が増えて儲かる、という流れです。
今回、ディズニーランドの待ち時間を調べている中でどの要素がどの待ち時間に影響しているのかを知りたいと思いました。
前回は、「美女と野獣 魔法のものがたり」の待ち時間だけに着目しましたが、今回は全体を見ようという内容になります。
実装
ランダムフォレストの実行
各要素に対する待ち時間をランダムフォレストにより予測してみます。
その際の、重要度でエッジの太さを求めて、グラフ化してみる事を試みます。
ランダムフォレストの実行のコードは以下です。
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import numpy as np
from sklearn.metrics import mean_squared_error as MSE
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.impute import SimpleImputer
frf = RandomForestRegressor()
# ランダムフォレストの結果を格納するリスト
edges = []
importance_threshold = 0.01 # 重要度の閾値(これより小さい関係は表示しない)
columns = ['splash_mountain', 'beauty_and_beast', 'happy_ride', 'monsters_inc',
'star_tuors', 'woodchuck_donald', 'woodchuck_daisy', 'mickey_house',
'minnie_style_studio', 'la_taverne_de_gaston', 'big_pop']
for target_col in columns:
y = shaped_df[target_col]
X = shaped_df.drop([target_col], axis=1)
# ランダムフォレストの実行
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X, y)
print(target_col, '決定係数:', model.score(X,y))
# 重要度が高い5つの特徴量を取得
feature_importances = pd.Series(model.feature_importances_, index=X.columns)
top_features = feature_importances.nlargest(5)
# エッジ情報を格納(target_colと各特徴量の関係)
for feature, importance in top_features.items():
if importance >= importance_threshold: # 重要度フィルタリング
edges.append((target_col, feature, importance))出力は以下のようになりました。
splash_mountain 決定係数: 0.9587482081978871
beauty_and_beast 決定係数: 0.9312782804271467
happy_ride 決定係数: 0.9655127525347255
monsters_inc 決定係数: 0.952834147017709
star_tuors 決定係数: 0.9524405715708658
woodchuck_donald 決定係数: 0.960319907168038
woodchuck_daisy 決定係数: 0.9603234062206942
mickey_house 決定係数: 0.9662015190822696
minnie_style_studio 決定係数: 0.9684021544918067
la_taverne_de_gaston 決定係数: 0.9168834441960294
big_pop 決定係数: 0.9201103854112727ネットワークグラフの作成
そして、次にこの結果をもとにグラフを作ってみます。
作成の際のグラフは以下のようなコードになります。
import japanize_matplotlib
# ネットワークグラフを作成
G = nx.Graph()
# 閾値を超えるエッジがあるノードのみ追加
nodes = set()
for source, target, weight in edges:
nodes.add(source)
nodes.add(target)
G.add_edge(source, target, weight=weight)
G.add_nodes_from(nodes) # ノードを追加
# 可視化
plt.figure(figsize=(20, 20))
pos = nx.spring_layout(G, seed=42) # 配置の固定
edges_weights = [G[u][v]["weight"] * 10 for u, v in G.edges()] # 重要度に応じた太さ
nx.draw(G, pos, with_labels=True, node_color="skyblue", edge_color="gray", width=edges_weights, font_size=10, node_size=2000,font_family='IPAexGothic')
plt.title("Feature Importance Network (Threshold Applied)")
plt.show()グラフは以下のようになりました。(各要素の名前についてはこちらの記事に記載しています。)
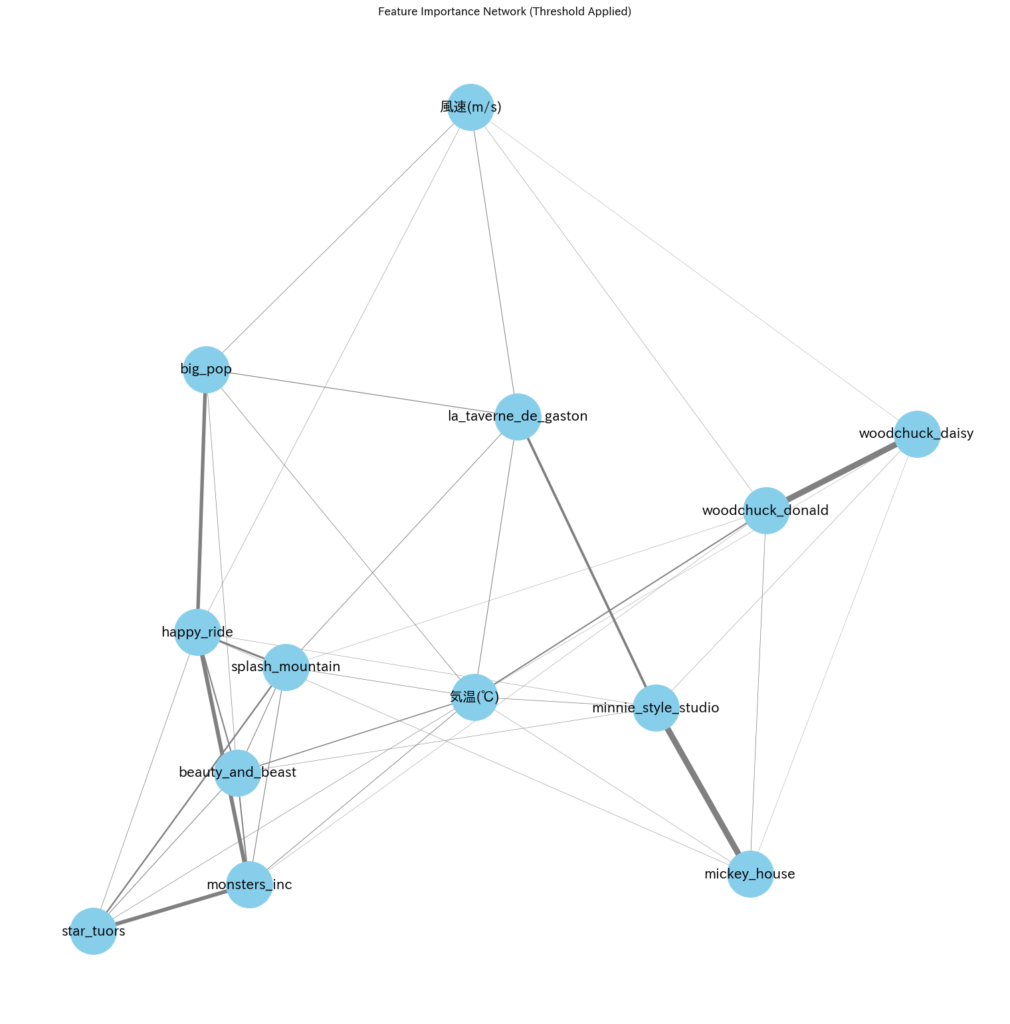
まとめと改善点
全体が混んでいれば、並ぶ時間も必然的に大きくなるのは当然といえば当然ですね。
必要なのはミクロの視点とマクロの視点だと思います。
つまり、ある条件下ではあるアトラクションの混雑具合が緩和されるかどうかというミクロの視点であったり、ディズニーランド全体がどれくらい混んでいるかというマクロの視点です。
この視点の考慮が今後の改善点で考えるべき一つの点です。
さらには、今回のデータに関しては以下のような改善点があります。
- 天気の情報パラメータが少ない
- イベント情報をダミー変数として使っていない
- ディズニーランド/シー側のデータも少ない
天気などのもともと予測されている情報に最も影響する待ち時間があれば、連鎖的にディズニーランド各アトラクションの待ち時間が連鎖的に予測できると考えています。


